Lista nr 1 - Wstęp (termin przesyłania sprawozdań: 13 III)

Ping:
Sprawdź za jego pomocą ile jest węzłów na trasie do (i od) wybranego, odległego geograficznie, serwera.
Uwaga: trasy tam i z powrotem mogą być różne.
Zbadaj jaki wpływ ma na to wielkość pakietu. Zbadaj jak wielkość pakietu wpływa na obserwowane czasy propagacji. Wyniki sprawdź dla różnych adresów DNS. Jeśli potrzeba, sporządź wykres. Zbadaj jaki wpływ na powyższe ma konieczność fragmentacji pakietów. Jaki największy niefragmentowany pakiet uda się przesłać. Dlaczego i od czego to zależy?
Przeanalizuj te same zagadnienia dla krótkich tras (do serwerów bliskich geograficznie). Określ "średnicę" internetu (najdłuższą sćieżkę, którą uda się wyszukać). Czy potrafisz wyszukać trasy przebiegające przez sieci wirtualne (zdalne platformy "cloud computing"). Ile węzłów mają ścieżki w tym przypadku?
Porównaj otrzymane wyniki przy pomocy Traceroute
Do czego służy WireShark; jak można tą funkcjonalność odnieść do Ping lub Traceroute.
Napisz sprawozdanie zawierające: opis programów, wywołania dla powyższych zagadnień z analizą wyników, wnioski dotyczące przydatności tych programów.

Lista nr 2 - Modelowanie niezawodności sieci (termin przesyłania sprawozdań: 10 IV)

. Przez N=[n(i,j)] będziemy oznaczać macierz natężeń strumienia pakietów, gdzie element n(i,j) jest liczbą pakietów przesyłanych (wprowadzanych do sieci) w ciągu sekundy od źródła v(i) do ujścia v(j).

Zaproponuj topologię grafu G ale tak aby żaden wierzchołek nie był izolowany oraz aby: |V|=20, |E|<30. Zaproponuj N oraz następujące funkcje krawędzi ze zbioru H: funkcję przepustowości 'c' (rozumianą jako maksymalną liczbę bitów, którą można wprowadzić do kanału komunikacyjnego w ciągu sekundy), oraz funkcję przepływu 'a' (rozumianą jako faktyczną liczbę pakietów, które wprowadza się do kanału komunikacyjego w ciągu sekundy). Pamiętaj aby funkcja przeplywu realizowała macierz N oraz aby dla każdego kanału 'e' zachodziło: c(e) > a(e).

Niech miarą niezawodności sieci jest prawdopodobieństwo tego, że w dowolnym przedziale czasowym, nierozspójniona sieć zachowuje T < T_max, gdzie: T = 1/G * Σ_{e} a(e)/(c(e)/m - a(e)), jest średnim opóźnieniem pakietu w sieci, Σ_{e} oznacza sumowanie po wszystkich krawędziach 'e' ze zbioru E, 'G' jest sumą wszystkich elementów macierzy natężeń, a 'm' jest średnią wielkością pakietu w bitach. Napisz program szacujący niezawodność takiej sieci przyjmując, że prawdopodobieństwo nieuszkodzenia każdej krawędzi w dowolnym interwale jest równe 'p'. Uwaga: 'N', 'p', 'T_max' oraz topologia wyjściowa sieci są parametrami.

Przy ustalonej strukturze topologicznej sieci i dobranych przepustowościach stopniowo zwiększaj wartości w macierzy natężeń. Jak będzie zmieniać się niezawodność zdefiniowana tak jak punkcie poprzednim (Pr[T < T_max])?

Przy ustalonej macierzy natężeń i strukturze topologicznej stopniowo zwiększaj przepustowości. Jak będzie zmieniać się niezawodność zdefiniowana tak jak punkcie poprzednim (Pr[T < T_max])?

Przy ustalonej macierzy natężeń i pewnej początkowej strukturze topologicznej, stopniowo zmieniaj topologię poprzez dodawanie nowych krawędzi o przepustowościach będących wartościami średnimi dla sieci początkowej. Jak będzie zmieniać się niezawodność zdefiniowana tak jak punkcie poprzednim (Pr[T < T_max])?

Napisz sprawozdanie zawierające opis zrealizowanych programów, komentarz do przeprowadzonych badań oraz wnioski.

FAQ do listy 2.
Umieszczam tu otrzymane mailowo pytania i odpowiedzi na nie. jeśli uważacie Pastwo, że takie odpowiedzi są zbyt mało precyzyjne lub coś innego jest niejasne, to proszę mnie atakować kolejnymi mailami.

1. Czy m - średnia wielkość pakietów w bitach ma być wartością zmienną, czy może być stała?
2. Czy przepustowość dla każdej krawędzi ma być inna (jeśli tak to w jakim zakresie), czy może być taka sama?
3. Czy zakładamy, że pakiety przechodzą najkrótszą drogą, czy tą najmniej obciążoną?
4. Czy przesyłanie pakietów ma następować pomiędzy dwoma konkretnymi (z góry ustalonymi) wierzchołkami, czy czy pomiędzy kombinacjami wierzchołków wybranych przez program?
5. Czy można korzystać z biblioteki "networkx" w celu rysowania grafów?
6. Czy funkcję a(e) należy obliczać na podstawie macierzy natężeń, a jeśli tak to w jaki sposób?
7. Jeżeli funkcja a(e) przyjmuje jako argument krawędź, to jak może ona realizować macierz N? W macierzy N rozróżniamy połączenia n(i,j) oraz n(j,i). Czy to oznacza, że jeśli mamy policzyć a(e), to bierzemy wartość maksymalną z n(i,j) i n(j,i)?
8. Z tego co zrozumiałem z FAQ, a(e) jest wyliczane na podstawie ścieżki, a nie krawędzi, czyli wtedy e oznaczałoby ścieżkę, a w przypadku c(e) e oznacza krawędź?
9. Czy w macierzy natężeń musimy zakładać, że wszyscy się ze sobą komunikują? Jeśli nie, to czy jest jakaś dolna granica na liczbę zer w macierzy?
10. Czy można uznać, że n(k,k)=0?

Ad 1. Parametr m należałoby uzmiennić. Naturalnie trzeba wykonać przez to dla każdego przypadku rozsądną (,,reprezentatywną") liczbę testów.
Ad 2. Także jest dobrze uzmiennić przepustowość. Należy ją w miarę rozsądnie dobrać do macierzy N i topologii sieci. Można np. policzyć średnią i potem przemnażać przez różne stałe z jakiegoś zakresu. Tu należy przetestować jakie są dobre. Potem ewentualnei na podstawie obserwacji można zmienic nieco podejście.
Ad 3. To jest kwestia definicji naszego modelu. Każdy z podanych modeli ma wady. W pierwszym np. niektóre krawędzie mogą się szybko zapchać. W drugim, ścieżka może być bardzo długa (np. dwa sąsiadujące wierzchołki w topologii cyklicznej mogą przesłać wtedy wiadomość niepotrzebnie przez cały cykl. Trzeba wypracować jakiś złoty środek. Można w tym celu jakoś wykorzystać stałą izoperymetyczną grafu (choć to już ambitny pomysł).
Ad 4. Macierz natężeń definiuje kto do kogo wysyła pakiety. Każdy pakiet musi w miarę rozsądnie wybrać ścieżkę podróży i każda krawędź tej ścieżki zostaje obciążona tymi pakietami, zmniejszając tym samym dostępną przepustowość.
Ad 5. Jak najbardziej. W Pythonie to raczej najlepsza biblioteka do grafów. Dobry jest też przykładowo javascriptowy Node.js. W Wolfram Mathematica też się da sprawnie działać na grafach.
Ad 6. Powiedzmy, że P(i,j) to zbiór wszystkich krawędzi wybranej ścieżki z wierzchołka v(i) do v(j). Wtedy a powinno być zadane wzorem:
a(e)=Σ_{i=1}^{|V|} Σ_{j=1}^{|V|} [|e ϵ P(i,j)|] n (i,j),
gdzie [|e ϵ A|] oznacza indykator zbioru A, tj. 1 tam, gdzie e ϵ A, a 0 w przeciwnym przypadku. Przy okazji trzeba zadbać o to, żeby dla żadnej krawędzi e, a(e) nie przekroczyło maksymalnej przepustowości c(e). Zatem tutaj zgodnie z Ad 4., trzeba wykombinować taki algorytm wybierania ścieżek (patrz Ad 3.), żeby to a raczej nie przekraczało c (nie trzeba szukać optymalnego algorytmu, ale takiego, który jest nie najgorszym przybliżeniem). Jeśli dla naszego algorytmu wyjdzie ostatecznie, że któraś krawędź niedomaga, to po prostu uznajemy to za porażkę dla zadanych parametów.
Ad 7. Macierz natężeń opisuje żadanie, tj. n_{i,j} podaje ile informacji v_i chce przekazać v_j. Ale może miedzy nimi nie istnieć krawędź i wtedy trzeba wysłać te dane po jakiejś scieżce. Każda z krawędzi na tej ścieżce jest wtedy obciążona całym pakietem (to wynika ze wzoru podanego na mojej stonie w Ad 6.). Co więcej n(i,j), z tej definicji, to nie to samo co n(j,i). W dwie strony można wysyłać różne informacje.
Ad 8. a(e) jest faktycznie wyznaczane na podstawie ścieżki. Jednak e oznacza krawędź, a do funkcji przepływu dal tej krawędzi, tj. a(e) wliczają się wszystkie ścieżki, które zawieraja tę krawędź, tzn. jest to suma wszystkich informacji, które przechodzą przez dana krawędź (to w zasadzie mówi ten wzorek z dwiema Sigmami. W szczególności, jeśli graf posiada most (https://pl.wikipedia.org/wiki/Most_(teoria_graf%C3%B3w), to przez ten most muszą przejść wszystkie pakiety, które mają krańce w dwóch spójnych składowych, które pozostają po usunięciu mostu.
Ad 9. Nie wszyscy muszą się ze sobą komunikować. Co więcej, komunikacja nie musi być symetryczna, tzn. n(i,j) nie musi być tym samym, co n(j,i). Jeśli chodzi o liczbę 0, to jest duża dowolność, ale raczej dobrze by było, żeby macierz byłą w miarę gęsta (rzędu |V|^2), np. przynajmniej 1/4 |V|^2 (to oznacza gęstość grafu na poziomie 1/2). Można tu rozważyć kilka różnych macierzy (np. o ~|V|log|V| niezerowych elementów albo nawet, gdy wszystkie wyrazy są niezerowe).
Ad 10. Oczywiście. Nie ma sensu, żeby ktokolwiek wysyłał pakiety do samego siebie.

Lista nr 3 - Ramkowanie (termin wysyłania sprawozdań: 8 V)

Napisz program ramkujący zgodnie z zasadą "rozpychania bitów" (podaną na wykładzie), oraz weryfikujący poprawność ramki metodą CRC. Program ma odczytywać pewien źródłowy plik tekstowy 'Z' zawierający dowolny ciąg złożony ze znaków '0' i '1' (symulujący strumień bitów) i zapisywać ramkami odpowiednio sformatowany ciąg do inngo pliku tekstowego 'W'. Program powinien obliczać i wstawiać do ramki pola kontrolne CRC - formatowane za pomocą ciągów złożonych ze znaków '0' i '1'. Napisz program, realizujacy procedure odwrotną, tzn. który odzczytuje plik wynikowy 'W' i dla poprawnych danych CRC przepisuje jego zawartość tak, aby otrzymać kopię oryginalnego pliku źródłowego 'Z'.
Napisz program (grupę programów) do symulowania ethernetowej metody dostępu do medium transmisyjnego (CSMA/CD). Wspólne łącze realizowane jest za pomocą tablicy: propagacja sygnału symulowana jest za pomoca propagacji wartości do sąsiednich komórek. Zrealizuj ćwiczenie tak, aby symulacje można było w łatwy sposób testować i aby otrzymane wyniki były łatwe w interpretacji.

Lista nr 4 - TCP/IP (termin: 29 V)

ts4.zip

Program Z2Sender wysyła w osobnych datagramach po jednym znaku wczytanym z wejścia do portu o numerze podanym jako drugi parametr wywołania programu. Jednocześnie drukuje na wyjściu informacje o pakietach otrzymanych w porcie podanym jako pierwszy parametr wywołania.
Program Z2Receiver drukuje informacje o każdym pakiecie, który otrzymał w porcie o numerze podanym jako pierwszy parametr wywołania programu i odsyła go do portu podanego jako drugi paramer wywołania programu.
Klasa Z2Packet, umożliwia wygodne wstawianie i odczytywanie czterobajtowych liczb całkowitych do tablicy bajtów przesyłanych w datagramie — metody: public void setIntAt(int value, int idx) oraz public int getIntAt(int idx). Wykorzystane jest to do wstawiania i odczytywania numerów sekwencyjnych pakietów.
Po skompilowaniu, można je uruchomić w terminalu w następujący sposób:
java Z2Receiver 6001 6000 & java Z2Sender 6000 6001 < plik.txt
W tej konfiguracji Z2Receiver powinien otrzymywać wszystkie pakiety w odpowiedniej kolejności i bez strat, a odsyłane przez niego potwierdzenia dochodzą do Z2Sender w taki sam (niezawodny) sposób. Program Z2Sender po zakończeniu transmisji musi być ręcznie przerwany (CTRL+C), bo wątek odbierający oczekuje na kolejne pakiety. Program Z2Receiver można zatrzymać przy użyciu poleceń ps (aby odczytać nr procesu) i kill (aby wysłać do procesu sygnał zakończenia). W Internecie każdy pakiet przesyłany jest niezależnie i w miarę dostępnych możliwości. W związku z tym pakiety wysyłane przez nadawcę mogą być tracone, przybywać z różnymi opóźnieniami, w zmienionej kolejności, a nawet mogą być duplikowane.
Program Z1Forwarder symuluje tego typu połączenie. Aby go użyć można wykonać (po zabiciu innych programów korzystających z portów 6000, 6001, 6002, 6003) następujące polecenia:
java Z2Receiver 6002 6003 & java Z2Forwarder 6001 6002 & java Z2Forwarder 6003 6000 & java Z2Sender 6000 6001 < plik.txt
W tej konfiguracji pierwszy Z2Forwarder przekazuje pakiety od Z2Sender do Z2Receiver, a drugi - w przeciwnym kierunku (może wystąpić pewne opóźnienie, zanim zaczną się pojawiać wyniki drukowane przez Z2Receiver i Z2Sender.)
Zadanie polega na takim wykorzystaniu potwierdzeń i numerów sekwencyjnych przez nadawcę i odbiorcę, aby odbiorca wydrukował wszystkie pakiety w kolejności ich numerów sekwencyjnych (nawet jeśli połączenie w obie strony odbywa się przez Z2Frowarder). Nadawca może przypuszczać, że pakiet nie dotarł do celu jeśli przez długi czas nie otrzyma potwierdzenia od odbiorcy. Może wtedy ten pakiet ponownie wysłać (retransmitować). Odbiorca może wykorzystywać numery sekwencyjne pakietów aby zorientować się czy ma prawo drukować dany pakiet, czy też musi czekać na brakujące wcześniejsze pakiety albo czy dany pakiet już był drukowany (np. jest duplikatem).

Lista nr 5 - HTTP (termin: 14 VI)
Plik server3.pl zawiera przykładowy program serwera protokołu HTTP.

Uruchom ten skrypt, przetestuj, zastanów się jak działa.
Nawiąż połączenie za pomocą przeglądarki internetowej.
Zmień skrypt (lub napisz własny serwer w dowolnym języku programowania) tak aby wysyłał do klienta nagłówek jego żądania.
Zmień skrypt (lub napisz własny serwer w dowolnym języku programowania) tak aby obsugiwał żądania klienta do prostego tekstowego serwisu WWW (kilka statycznych ston z wzajemnymi odwołaniami) zapisanego w pewnym katalogu dysku lokalnego komputera na którym uruchomiony jest skrypt serwera.
Przechwyć komunikaty do/od serwera za pomocą analizatora sieciowego - przeanalizuj ich konstrukcję.
Napisz zwięzłe sprawozdanie.

Zadanie na ocenę ,,celująco''(jedno do wyboru dla osób, które uzyskają średnią za 5 list, przynajmniej 4.8):
Zadanie 1. — Uogólnienie listy nr 2
Rozważmy model sieci, w którym czas podzielony jest na interwały, których (asymptotyczna) średnia długość wynosi T. Zakładamy, że długość przedziału losujemy z rozkładu t_i=U_1-U_2, gdzie U1,U2 mają rozkłady jednostajne na [0,T/2]. Długości interwałów są zmienne, ze względu na zmiany średnich długości opóźnień. Pomijamy je w rozważaniach, bazując jedynie na funkcjach przepływu a oraz przepustowości c.
Załóżmy wpierw, że komputery (węzły) wykorzystane w połączeniach są niezawodne oraz, że funkcja niezawodności w i-tym interwale czasowym dla każdej krawędzi e(j,k) wyraża sie wzorem h_i(e(j,k))=1-p(e(j,k))-t_i*q(e(j,k)), gdzie p jest z góry zadaną funkcją prawdopodobieństwa, a q jest funkcją parametru, który jest wprost proporcjonalny do przepływu a_i(e(j,k)) w danej krawędzi i interwale czasowym i (zakładamy, że współczynnik proporcjonalnoości jest stały w czasie i taki sam dla wszystkich krawędzi). Podać interpretację wzoru, zbadać minimum i maksimum i zaproponować rozsądne wartości p i q do testowania. Załóżmy przy tym, że niezawodność każdej krawędzi musi wynosić co najmniej 0,75.
Niech R(e(j,k)) będzie czasem naprawy uszkodzonej krawędzi e(j,k), który powinien być zamodelowany rozkładem wykładniczym z pewnym parametrem lambda(e(j,k)) (warto spojrzeć szczególnie na 'Mean' w 'Properties' i 'Generating exponentional variables'). Dla uproszczenia zakładamy, że krawędź psuje i naprawia się zawsze na koniec interwału czasowego. Dobrać rozsądne lambda do p i q.
Przetestować 3 modele sieci (graf Petersena (zrównoważony), |G|=10, |E|=15; graf kołowy (zrównoważony oraz centralny), |G|=9, |E|=16).
We wszystkich modelach zakładamy, że każdy komputer chce przesyłać do wszystkich innych jakiś komunikat konkretnego ustalonego rozmiaru, więc macierz natężeń N ma wszystkie elementy takie same.
W modelach zrównoważonych zakładamy, że funkcje bazowego prawdopodbieństwa awarii p(e(j,k)) oraz przepustowości c(e(j,k)) są stałe ze względu na krawędzie i interwały.
W modelu centralnym zakładamy, że funkcja p(e(j,k)) jest kilka razy mniejsza dla "szprych", prowadzących do centralnego wierzchołka, niż na obwodzie koła (zakładamy, że dla wszystkich ,,szprych" wartości są takie same, podobnie dla kanałów na obwodzie koła) oraz c(e(j,k)) dla ,,szprych", są kilka razy większe, niż na obwodzie koła (przetestować przykładowo współczynniki od 1/8 do 1/2 oraz od 2 do 8, odpowiednio, niekoniecznie odwrotne wartości dla obu parametrów). Zastanowić się dlaczego tak powinno być. Dostosować macierz natężeń N do zmian funkcji p i c.
Przeprowadzić symulacje procesów Markowa awarii—naprawy dla powyższych modeli, dla różnych parametrów p, q, lambda oraz współczynników proporcjonalnosci dla funkcji c w modelu centralnym.
Rozważyć średnią liczbę interwałów w poszczególnych stanach dla każdego modelu z osobna.
Stan -1 oznacza całkowitą awarię, czyli graf został rozspójniony lub przepływ w którejś krawędzi przekroczy przepustowość danego kanału.
Stan 0 oznacza, że wszystkie kanały są sprawne i nie nastąpiła całkowita awaria.
Stan 1 oznacza, że jeden kanał nie działa w danym interwale i nie nastąpiła całkowita awaria, Stan 2 - nie działają dwie krawędzie, ale system nie zawiódł, itd.
Znaleźć rozsądne oszacownie na liczbę stanów w każdym modelu. Przeprowadzić symulacje dla wszystkich modeli.
Oszacować prawdopodobieństwo, że podczas całej próby (np. n=2000 interwałów) nastąpiła całkowita awaria. Przeprowadzic kilka eksperymentów. Rozważyć heurystycznie, co mogłoby się dziać, gdyby rozważać awarie węzłów. Napisać sprawozdanie.

Zadanie 2.— Uogólnienie zadania z listy nr 3
Napisać grupę programów do symulowania ethernetowej metody dostępu do mediów transmisyjnych (CSMA/CD).
Wspólne łącze realizowane jest przy pomocy tablic: każde urządzenie jest umieszczone na końcu kabla, propagacja sygnału symulowana jest za pomoca propagacji wartości do sąsiednich komórek.
Rozważamy 2 modele.
W pierwszym, urządzenia połączone są na wzór grafu kołowego. Każdy węzeł grafu symbolizuje urządzenie, a krawędź — kabel losowej długości (tablice są różnych długości).
Należy przetestować różne liczby komputerów. Założyć, że kolizje mogą być wykrywane jedynie przez urządzenia. Jak rozwiązać problem wysyłania wiadomości do samego siebie?
W drugim modelu rozważyć sytuację zadaną przez graf gwiaździsty. Jedno centrum — serwer, a pozostałe węzły to urządzenia podłączone bezposrednio do serwera. Każde urządzenie chce przesłać wiadomosć do pozostałych. Gdy serwer otrzyma jakąś wiadomość, to przejmuje rolę nadawcy. Znaleźć techniczne rozwiazanie tego problemu. Przeprowadzić symulacje dla różnych liczb urządzeń oraz średnich długości kabli w obu modelach i napisać sprawozdanie.

Ogóle uwagi odnośnie sprawozdań:

Bardzo często pojawiającym się błędem językowym (ok. 95% prac) jest używanie słowa ,,ilość'' w nieodpowiednim kontekście. Słowo to jest zarezerwowane dla opsiu rzeczy niepoliczalnych, jak przykładowo ciecze. Mamy zatem np. ilość wody, mleka czy masła (tu w kg). Jeśli opisujemy węzły, routery, bajty, czy inne policzalne rzeczy (izomorficzne z podzbiorem liczb naturalnych w skali makroskopowej), powinniśmy użyć słowa liczba (w szczególności: liczba liczb pierwszych jest jak najbardziej poprawnym określeniem).
Dobrym nawykiem jest, aby w miarę możliwości nie zamieszczać obrazków, czy tabel, o ciemnym tle, żeby nie tracić zbyt wielu zasobów przy okazji drukowania.
Ponadto, gdy mamy jakieś załączniki typu rysunek, obraz, tabela, rycina, algorytm, to dobrze jest je podpisać (caption), czyli zrobić zwięzły opis tuż przy załączniku, wraz z podaniem nazwy i numeru, np. ,,Tabela 3. Wyniki zapytań ping dla wybranych serwerów wraz ze średnim czasem odpwiedzi i ich odchyleniem standardowym. Liczba prób=40, wielkość pakietów=64B". Potem można się bezpośrednio odnieść do danego załącznika(tak zwane referencje), żeby było jasne na podstawie czego wnioskujemy (czasem poszukiwania źródeł wniosków zajmowały mi ponad godzinę na jedno sprawozdanie, a bywało, że ich nie znajdowałem ostatecznie).
Często w sprawozdaniach przytaczacie Państwo zewnętrzną wiedzę. Normalnie w takiej sytuacji stosuje się cytowanie. Na potrzeby tego kursu możemy uznać to za niekonieczne. Ale przed umieszczeniem takiej informacji, warto najpierw sprawdzić, czy na pewno jest ona prawdziwa, poszukując w wielu niezależnych od siebie źródłach. Bywało, że niektóre wnioski były oparte na nieprawdziwych informacjach.
Państwa sprawozdania opierają się na pewnych badaniach. Z jednej strony mogą być one postrzegane jak eksperymenty fizyczne, jeśli otrzymywane wyniki się wcale nie różnią. Część wyników otrzymywanych przez fizyków jednak jest akceptowana przy okoliczności błędów pomiarowych. Jednak wtedy najczęściej znany jest z góry maksymalny błąd pomiarowy urządzeń mierniczych. Urządzenia można kalibrować i otrzymywać małe średnie błędy. Jeśli jednak otrzymujemy różne wyniki i nie mamy znaczących błędów pomiarowych, to należy zastosować podejście statystyczne. Znaczna większość przyjmowała coś na wiarę, bo dla prau przypadków się zgadza. Statystyka w pierwszej połowie XX w. była precyzyjną dziedziną matematyki. Przez lata jednak ewoluowała i w szczególności wypączkowała pewną odmianę – statystykę opisową – z której to poważni statystycy nie są do końca zadowoleni. Ta ,,Statystyką dla bystrzaków'' jest próbą zaadaptowania trudnej dziedziny matematyki do zjadliwej dla przeciętnego człowieka postaci. Jednak, by bardzo dobrze posługiwać się ,,slangiem'' statystyki opisowej, należy wystarczająco rozumieć to co za nią się kryje. Porządne jej zrozumienie wymaga jednak dobrej znajomości teorii miary, więc nie zamierzam się w to tutaj zagłębiać. Bardzo duża część z nas jest pod wpływem utartych określeń, zasłyszanych np. od centrów badań społecznych (które czasem nawet nie zatrudniają statystyków). Te zasłyszane frazy często posiadają dosyć dokładną interpretację, lecz często są one nadużywane lub źle interpretowane, przez co łatwo tu o wprowadzenie w błąd. Dlatego poniżej umieszczę kilka ogólnych zasad najbardziej podstawowoych rozumowań statystycznych. Liczę, że zostaną one jakkolwiek uwzględnione przy kolejnych Państwa sprawozdaniach. Myślę, że to też cenna wiedza użyteczna (żeby nie dawać się oszukiwać albo, żeby umieć się wypowiadaćw tym języku).
Bardzo często słyszymy określenie, że badanie zostało przeprowadzone na reprezentatywnej próbie. Co to znaczy? Statystyka najczęściej testuje pewne hipotezy. Tak zwane hipotezy zerowe, przy opcjonalnej hipotezie alternatywnej (dopełnieniu hipotezy zerowej). Jest to sprawdzane przy pomocy tak zwanych testów statystycznych. I zazwyczaj to od ich określenia zależy jaka powinna być wielkość próby (liczby osób, przebadanych egzamplarzy lub liczby badań). Z reguły jednak się zakłada, że próba ma wielkość minimum 40 (większość testów praktycznie nie działa dla mniejszych, choć istnieją testy desygnowane dla prób o wielkości od 10 do 40). Lecz czy to wystarczy, żeby mówić, że próba jest reprezentatywna? Wystarczy się zastanowić, czy jeśli spytamy losowych 40 Polaków o wiek, czy będziemy mieć orientacyjną wiedzę na temat rozkłądu wieku Polaków? Raczej nie. Próby powinny być takie, żeby po powtórzeniu eksperymentu rozkład próby był zbliżony (w jakimś sensie). W kontekście sprawozdań, wypadałoby, zeby wykonywać zatem sporą liczbę testów (u Państwa często to było 4 lub 5).
Podobna kwestia to rzetelne dobór eksperymentów. Jeśli wysyłamy zapytania tylko do serwera rządu w Burkina Faso (w kontekście pinga), to jest tak, jakbyśmy ankietowali tylko mieszkańców Niepołomic o ich wiek. Intuicyjnie nie będzie to dobrym odwzorowaniem wieku w całej Polsce (różnorodność źródeł). Podobnie, w sprawozdaniach powinniśmy uzmienniać wiele parametrów, ale na tyle, żeby dało sie cos na ich podstawie wywnioskować. Najwygodniej początkowo zmieniać jeden parametr jednocześnie. Można uwzględniać nawet wszystkie parametry naraz (tak zwane modele analizy wariancji ANOVA), ale to wymaga dodatkowej wiedzy.
Ponadto w poważnej statystyce nie ma mowy o przyjmowaniu hipotez. Można co najwyżej nie odrzucić jakiejś hipotezy (zerowej) na jakimś poziomie ufności (najczęściej 95% lub 99%) albo ją odrzucić. W pierwszej opcji, test statystyczny pokazuje, że z prawdopodobieństwem co najmniej wynoszącym poziom ufnosci hipoteza (zerowa) sie potwierdza dla danej próby. Mówi się wtedy, ze nie ma podstaw do odrzucenia hipotezy zerowej. W kontekście naszych sprawozdań sprawa wygląda nieco inaczej, bo najpierw wykonujemy badania, a potem stawiamy hipotezę (którą powinniśmy dopiero przetestować), ale tutaj nie czuję potrzeby powtórnego zawierania tego w sprawozdaniu. Ze względu na to, że nie operują Państwo w znacznej większości dobrą wiedzą statystyczną, to nie ma sensu wymagać poprawnego testowania hipotez zgodnie ze status artis. Natomiast będę wymagał, żeby w przypadku, gdy ktoś chce odrzucić jakąś hipotezę, gdy może ona się wydawać prawdziwa (tzw. błąd I rodzaju), to żeby to poparł wystarczająco dużą liczbą prób. Czyli jak mamy jakieś wątpliwości, to róbmy znacznie więcej prób. Podobnie, gdy chcemy zatwierdzić poprawność hipotezy zerowej, a niektóre wyniki nam nie pasują (błąd II rodzaju), to musimy zrobić więcej prób albo wyjaśnić, dlaczego niektórych danych nie powinniśmy analizować jako outliers. W tym ostatnim kontekście prawie nikt nie zauważył, że niektóre zapytania pingiem dawały znacznie większe czasy, zwiększajac przy tym średni czas propagacji oraz wariancję wyników, przez co pobrane dane nie były zbierane w mozliwie jednakowych warunkach. Warto też było sie odnieść jak często się takie istotne odchylenia zdarzały.
Niemal wszyscy badając wpływ rozmiaru wysyłanych pakietów na czas ich propagacji, badali, co prawda dla różnych serwerów, ale zazwyczaj tylko 2 lub 3 przykładowe wartości rozmiaru pakietów. Porządna analiza powinna wykazać dokładny wpływ rozmiaru na propagację (czy jest liniowy, kwadratowy, a może jeszcze inny). U Państwa najczęściej odpowiedzią było, czy wpływ jest, czy go nie ma. A niektórzy wnioskował dla dwóch wartości i wychodziło im, że wpływu nie ma. Dla zobrazownia zamieszczam poniższy wykres:

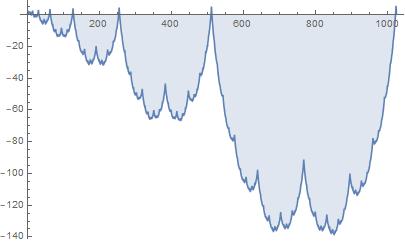
Figura 1. Wykres funkcji f(n), która zwraca sumę jedynek w binarnych reprezentacjach wszystkich liczb naturalnych nie większych, niż n, pomniejszonej o nlg(n)/2.
Jeśli będziemy testować hipotezę, że wartość funkcji f się nie zmienia, to możemy dojść do błędnych wniosków, jeśli za n przyjmować będziemy liczby diadyczne (potęgi liczby 2). Dlatego trzeba bardzo uważnie testować niektóre hipotezy. Szczególnie, jeśli dotyczą dość specyficznych wielkości (jak MTU czy pakiety o wielkościach diadycznych).
Zwracam się także z prośbą o uważne czytanie treści zadań. Często Państwo zapominacie o czymś. Warto przed wysłaniem sprawozdania jeszce raz sprawdzić, czy jest wszystko, czego potrzeba.
W paru przypadkach było widać, że komuś nie chciało się pisać i niektóre wnioski są tylko same dla siebie. Teraz jest czas, kiedy Państwo doświadczają prawdziwego studiowania, czyli samodzielnej analizy problemów. Chyba warto to wykorzystać dla samorozwoju i przyłożyć się nieco bardziej.

Zachęcam również do spojrzenia na podobne, bardziej językowe i techniczne uwagi, przygotowane przez jednego z pracowników naszego Wydziału: [PDF].