Zadania i rozwiązania

Zadanie 1.0

Wyznacz punktu skupienia ciągu $a_n = (-1)^n \frac{\log_2(2^n+3^n)}{n}$.
Rozwiązanie:
Niech $b_n = \frac{\log_2(2^n+3^n)}{n}$. Mamy (z twierdzenia o trzech ciągach) $\lim_n b_n = \log_2(3)$. Zatem $\lim_n a_{2n} = \lim_n b_{2n} = \log_2(3)$ oraz $\lim_n a_{2n+1} = (-1)\cdot\lim_n b_{2n+1} = -\log_2(3)$. Punktami skupienia ciągu $a_n$ są więc liczby $-\log_2(3)$ oraz $\log_2(3)$.

Zadanie 1.1

Wyznacz punkty skupienia ciągu $a_n = \sqrt[n]{2^n+3^n}$.
Rozwiązanie:
Niech $b_n = \sqrt[n]{2^n+3^n}$. Mamy (z twierdzenia o trzech ciągach) $\lim_n b_n=3$. Zatem $\lim_n a_{2n} = \lim_n b_{2n} = 3$ oraz $\lim_n a_{2n+1} = (-1)\cdot\lim_n b_{2n+1} = -3$. Punktami skupienia ciągu $a_n$ są więc liczby $-3$ oraz $3$.

Zadanie 2.0

Niech $A=\{(x,y):-1\leq x\leq 2 \land |y|\leq |x(2-x)|\}$. Oblicz powierzchnię zbioru $A$.
Rozwiązanie:
Należy wyznaczyć pole nastepującej figury:

Pole to jest równe $2\left(\int_{-1}^{0} x(x-2) dx + \int_{0}^{2}x(2-x) dx\right) = \ldots = \frac{16}{3}$.

Zadanie 2.1

Niech $A=\{(x,y):0\leq x\leq 2\pi \land |y|\leq |\sin(2x)|\}$
Rozwiązanie:
Należy wyznaczyć pole nastepującej figury:

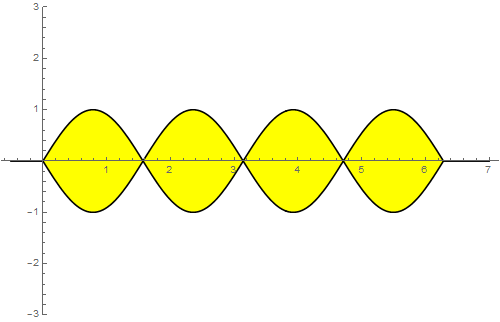
Pole to jest równe $8\left(\int_{0}^{\pi/2}\sin(2x) dx\right) = \ldots = 8$.

Zadanie 3.0

Załóżmy, że $\int f(x)dx = F(x) + C$. Oblicz $\int(x^2\ln(x) +f(2x+1))dx$.
Rozwiązanie:
Metodą całkowania przez części otrzymujemy $\int x^2\ln(x) dx =\frac{1}{3} x^3 \log (x)-\frac{x^3}{9}+C$. Ponadto $\int f(2x+1) dx =_{u=2x+1} \int f(u) \frac12 du = \frac12 F(u)+ D = \frac12 f(2x+1)+D$. Zatem szukana całka jest równa: $$ \frac{1}{3} x^3 \log (x)-\frac{x^3}{9} + \frac12 f(2x+1) + C~. $$

Zadanie 3.1

Załóżmy, że $\int f(x)dx = F(x) + C$. Oblicz $\int(x^2\sin(x) +f(2x+1))dx$.
Rozwiązanie:
Metodą całkowania przez części otrzymujemy $\int x^2\sin(x) dx =2 x \sin (x)-\left(x^2-2\right) \cos (x)+C$. Ponadto $\int f(3x+1) dx =_{u=3x+1} \int f(u) \frac12 du = \frac13 F(u)+ D = \frac13 f(3x+1)+D$. Zatem szukana całka jest równa: $$ 2 x \sin (x)-\left(x^2-2\right)\cos(x) + \frac13 f(3x+1) + C~. $$

Zadanie 4

Zbadaj ciągłość i rózniczkowalność funkcji określonej wzorem $$ f(x) = \begin{cases} 0 &: x\leq 0 \\ x\ln(x) &:x>0\end{cases} $$
Rozwiązanie:
Funkcja $f$ jest różniczkowalna na $\RR\setminus\{0\}$. Należy się więc przyjrzeć zachowaniu funkcji $f$ w punkcie $0$. Z tego, że $$ \lim_{x\to 0+}f(x) = \lim_{x\to 0+}\frac{\ln(x)}{x^{-1}} =^H \lim_{x\to 0+} \left(- \frac{x^2}{x}\right) = 0 $$ wynika, że $f$ jest ciągła w $x=0$. Następnie mamy $$ f'_+(x) =\lim_{x\to 0+} \frac{f(x)-f(0)}{x-0} = \lim_{x\to 0+} \ln(x) = -\infty $$ wynika, że $f$ nie jest różniczkowalna w punkcie $0$.

Zadanie 5.0

Zbadaj przebie zmienności funkcji $$ f(x) = \frac{\sqrt{5}-x}{2-x^2} $$
Rozwiązanie:
Dziedziną funkcji jest zbiór $\RR\setminus\{-\sqrt{2},\sqrt{2}\}$. Analiza jest standardowa (nie podaję wszystkich szczegółów). Mamy $$ f'(x) = -\frac{x^2-2 \sqrt{5} x+2}{\left(x^2-2\right)^2} $$ Punkty zerowe pochodnej: $x_0=\sqrt{5}-\sqrt{3}, x_1=\sqrt{3}+\sqrt{5}$. Oto wykres funkcji $f$:

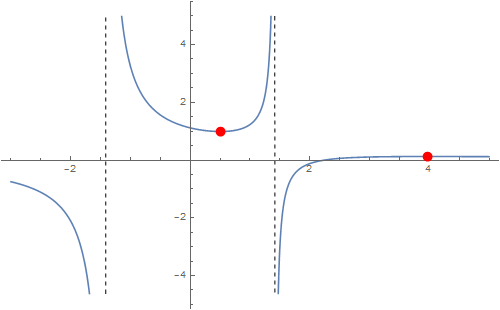
Czerwonymi krokpami są zaznaczone lokalne minimim oraz lokalne maksimum.

Zadanie 5.1

Zbadaj przebie zmienności funkcji $$ f(x) = \frac{\sqrt{10}-x}{2-x^2} $$
Rozwiązanie:
Dziedziną funkcji jest zbiór $\RR\setminus\{-\sqrt{2},\sqrt{2}\}$. Analiza jest standardowa (nie podaję wszystkich szczegółów). Mamy $$ f'(x) = -\frac{x^2-2 \sqrt{10} x+2}{\left(x^2-2\right)^2} $$ Punkty zerowe pochodnej: $x_0=\sqrt{5}-\sqrt{3}, x_1=\sqrt{3}+\sqrt{5}$. Oto wykres funkcji $f$:

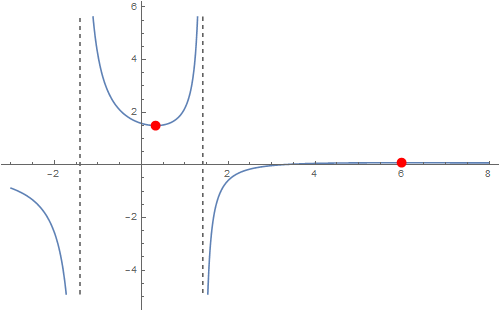
Czerwonymi krokpami są zaznaczone lokalne minimim oraz lokalne maksimum.

Zadanie 6.0

Wyznacz takie $q$, że $\sum_{n\geq 2}q^n = 2$.
Rozwiązanie:
Mamy $\sum_{n\geq 2}q^n = q^2 \sum_{n\geq 0}q^n = \frac{q^2}{1-q}$. Równanie $\frac{q^2}{1-q} = 2$ przekształcamy do $q^2 = 2 - 2q$, czyli $q^2+2q-2=0$. Ma ono dwa rozwiązania: $q_0 = -\sqrt{3}-1$ oraz $q_1 = \sqrt{3}-1$. Mamy $|q_0| \gt 1$ oraz $|q_1| \lt 1$. Jedynym $q$ takim, że $\sum_{n\geq 2}q^n = 2$ jest więc liczba $q_1$.

Zadanie 6.0

Wyznacz takie $q$, że $\sum_{n\geq 1}q^{2n} = 2$.
Rozwiązanie:
Mamy $\sum_{n\geq 1}q^{2n}$ = $\sum_{n\geq 1}(q^2)^n$ = $q^2 \sum_{n\geq 0}(q^2)^n$ = $\frac{q^2}{1-q^2}$. Równanie $\frac{q^2}{1-q^2} = 2$ przekształcamy do $q^2 = 2 - 2q^2$, czyli $3q^2=2$. Ma ono dwa rozwiązania: $q_0 = -\sqrt{2/3}$ oraz $q_1 = \sqrt{2/3}$. Mamy $|q_0| \lt 1$ oraz $|q_1| \lt 1$. Szukanymi liczbami są więc obie liczby $q_0$ oraz $q_1$.