01.03.2017: Wstęp

1. Hello world dla Big Data: word-count problem.
2. Indeks TF.IDF:
   
   1. $D_1, \ldots, D_m$ - zbiór dokumentów
   2. $w_1, \ldots, w_n$ - zbiór słów występujących w dokumentach
   3. $n_{i,j}$ = liczba wystąpień słowa $w_i$ w dokumencie $D_j$
   4. $TF_{i,j} = n_{i,j}/(\sum_a n_{a,j})$ (term frequency)
   5. $IDF_i = \log_2(m/\{j: w_i \in D_j\})$ (inverted document frequency)
   6. $TF.IDF_{i,j} = TF_{i,j} \cdot IDF_i$
3. Python: wykorzystanie funkcji map

   list(map(lambda x:x*x,range(1,11)))
   

4. Silnia w języku Scala:

   def Factorial(n:Int):BigInt = {
     require(n>=0)
     if (n==0) 1 else Range(1,n+1).map(BigInt(_)).reduce(_*_)
   }
   

5. Wartość oczekiwana $\geq 2$-kolizji (przykład Ullmana): $E[L] \approx \frac12 (p T R)^2$, gdzie $p$ = prawdopodobieństwo przebywania w jednym dniu w hotelu, $T$ = liczba dni obserwacji, $R$ = średnia liczba miejsc w hotelu.
6. Funkcje haszujące. Przykład $$ h(x) = \left((a_0+a_1 x + a_2 x^2 + \ldots + a_{k-1}x^{k-1}) \mod p \right) \mod L $$
7. Paradoks urodzinowy: $E[L] = \sqrt{\frac{\pi n}{2}} + \frac23 + O(n^{-\frac12})$
8. ZADANIE: zainstaluj Skalę i zacznij bawić się konsolą REPL. Przydatne na początku polecenia:
   • :q - wyjście
   • :help
   • :load - zaladowanie skryptu
   • :save - zapisanie sesji
   • obiekt.<tab> - lista dostępnych metod

08.03.2017: Model obliczeń Map-Reduce

1. Podstawowy model: procesy typu MAPPER - funkcja haszująca - procesy typu REDUCER.
2. Mnożenie macierzy przez wektor przechowywany w pamięci:
   MAPPER $(i,j,a_{ij}) \to (i,a_{i,j}x_j)$,
   REDUCER: $(i,L) \to (i, sum(L))$
3. Operacje teorio-bazowe (suma, przekrój, różnica)
   MAPPER: $a \in A \to (a,1)$, $b \in B \to (b,2)$
   1. suma: REDUCER: $(a,L) \to a$
   2. przekrój: REDUCER: $(a,L) \to a$ jeśli $|L|=2$
   3. różnica: REDUCER: $(a,L) \to a$ jeśli $L=[1]$
4. Złączenie $R(a,b) \bowtie_b S(b,c)$: MAPPER: $(a,b)\in R \to (b,(1,a))$, $(b,c)\in S \to (b,(2,c))$, REDUCER: dla każdej pary $(b,L)$ porządkuje $L$ względem pierwszej współrzędnej, przedstawia $L$ w postaci $$ [(1,a_1),(1,a_2),\ldots,(1,a_n)] \quad || \quad [(2,c_1), (2,c_2), \ldots,(2,c_m)] $$ i generuje $n\cdot m$ par $$ \{(a_i,c_j): 1\leq i \leq n \land 1\leq j \leq m\} $$
5. COMBINER: odpowiednik REDUCER'a działający po stronie MAPPER'a; działanie $\theta$ stosowane do list musi być łączne i przemienne.
6. Operacja $(n,s)\oplus(m,t) = (n+m, \frac{ns+mt}{n+m})$ jest łączna i przemienna; możemy ją wykorzystywać do obliczania średniej.

15.03.2017: Model obliczeń Map-Reduce

1. Two Side Chernoff inequality: Jeśli $X\sim Bin(n,p)$, $\mu = np$ i $\varepsilon>0$ to $$ \Pr[|X-\mu|\geq \varepsilon \mu] \leq 2 \exp(-\frac13 \varepsilon\mu) $$
2. Iloczyn macierzy - I:
   1. Mapper: $(A,i,j,a_{ij}) \to (j,(1,i,a_{ij}))$, $(B,j,k,b_{jk}) \to (j,(2,k,b_{jk}))$
   2. Reducer: $(j,L)$ przekształca w listę $(i,j,k, a_{ij}b_{jk}): i,k=1,\ldots,n$
   Wymaga ponownego użycia MapReduce.
3. Iloczyn macierzy - II:
   1. Mapper: $(A,i,j,a_{ij}) \to ((i,k),(1,j,a_{ij}), k=1\ldots,n$, $(B,j,k,b_{jk}) \to ((i,k),(2,j,b_{jk}), i=1\ldots,n$
   2. Reducer: $((i,k),L) \to (i,j,\sum L)$
4. Podobne obiekty: wejście $(i,A_i)$; ustalamy $g$; symulujemy podział na $\{0,\ldots,g-1\}^2$ grup; bierzemy pomocniczą funkcję haszującą $h: \ZZ\to \{0,\ldots,g-1\}$:
   1. Mapper: $(i,A_i) \to \{(\{h(i),v\},(i,A_i)): v\in\{0,\ldots,g-1\}, v\neq h(v)\}$
   2. Przykład k-gramu pliku tekstowego: tniemy tekst $a_1a_2\ldots a_n$ na $$ \{a_{i}\ldots a_{i+k-1}: i=1,\ldots,n-k+1\} $$
5. Podobieństwo Jaccarda:
   $$ S(A,B) = \frac{|A\cap B|}{|A \cup B|} $$
   Funkcja $d(A,B) = 1-S(A,B)$ jest odległością [zadanie]
6. Niech $\Omega=\{\omega_1,\ldots,\omega_n\}$. Niech $A, B \subseteq \Omega$. Dla permutacji $\pi$ zbioru $\Omega$ określamy $$ h_\pi(A) = \min\{k: \omega_{\pi(k)} \in A\} $$
7. Tw. Dla $A,B \subseteq \Omega$ mamy
   $$ \Pr[h_\pi(A) = h_\pi(B)] = S(A,B)~. $$
   (permutacje $\pi$ wybieramy z prawdopodobieństwem jednostajnym na zbiorze wszystkich permutacji $\Omega$).

22.03.2017: Locality Sensitive Hashing

1. Technika MIN_HASH: Niech $h:\Omega \to \{0,\ldots,L\}$ będzie losową funkcją haszującą. Dla $A\subseteq \Omega$ takich, że $|A| \leq \sqrt{L}$ określamy $$ h^*(A) = \min\{h(a):a\in A\} $$ Wtedy $$ Pr_h[h^*(A)=h^*(B)] \sim \frac{|A\cap B|}{|A \cup B|} (= s(A,B))~. $$
2. Wybieramy niezależne $h_1, \ldots , h_k$ funkcje haszujące. Szkicem $A$ nazywamy ciąg $$ sketch(A) = [h_1^*(A),h_2^*(A),\ldots,h_k^*(A)] $$
3. Wniosek: $$ E[|\{i:sketch(A)_i=sketch(B)_i\}|] = k \cdot s(A,B)~. $$
4. Wzmocnienie. Dzielimy $k$ na $l$ bloków rozmiaru $b$ (mamy $k = b\cdot l$). Rozbijamy szkice na bloki: $$ sketch(A) = [b_1(A)|b_2(A)|\ldots|b_l(A)] $$ Dla dowolnych $A$, $B$ mamy $$ Pr[(\exists i)(b_i(A)=b_i(B))] = 1 - (1- s(A,B)^b)^l $$ Projekt MapReduce: $$ MAPPER: \quad (i,[b_1|b_2|\ldots|b_l]) \to \{ (b_i,(i,[b_1|b_2|\ldots|b_l])): i =1\ldots,l\} $$
5. Tw. Jeśli dla podobieństwa $s(\cdot,\cdot)$ istnieje LSH, to funkcja $d(x,y) = 1-s(x,y)$ jest metryką.
6. Odległość cosinusowa: rodzina LSH dla $\{x\in\RR^n:||x||=1\}$: $$w^*(x) = sgn(x \circ w)~,$$ gdzie $w$ jest losowym wektorem z $\RR^n$.
7. LHS dla odległości Hamminga na $\{0,1\}^n$: $h_i(x) = x_i$ ($i=1,2,\ldots,n$)

29.03.2017: Streaming - I

1. MAJORITY ALGORITHM (Boyer-Moore,1981)
   Zakładamy, że jest $a$ takie, że $f_a = |\{i\in\{1,\ldots,n\}:a_i = a\}| > \frac{n}{2}$:

   INIT: c=0;m=nil;
   procedure add(x){
     if (c==0) {m=x}
     if (x==m) {c++} else {c--}
   } 
   OUT: m
   

   Twierdzenie: Ten algorytm działa poprawnie.
   Dowód (hint): Rozważamy funkcję $d_i = c$ jeśli $a_i = best$ oraz $d_i = -c$ jeśli $a_i\neq best$.
2. MISRA-GRIES SUMMARIES (1982)

   INIT: A = Map[String->Int]()
   procedure Add(x){
     if (A.hasKey(x)) A(x)++ else A += (x,1);
     if (A.length>=k){
       zmniejsz wartości wszystkich kluczy o 1;
       usuń z A te krotki, których wartości są równe 0
     }
   }
   OUT: A
   

   Twierdzenie: Dla każdego $x$ mamy $f_x - \frac{n}{k} \leq A(x) \leq f_x$
   Dowód (hint). Pokazujemy, że liczba odpaleń podprocedury czyszczącej jest mniejsza lub równa $\frac{n}{k}$.
3. COUNT-MIN SKETCH (G. Cormodore, S. Muthukrishnan, 2003):
   Wybieramy $B$ niezależnych funkcji haszujących h(0,*),...,h(b-1,*) o wartościach w zbiorze $\{0,\ldots,L-1\}$. Rezerwujemy pamięć na macierz A[0...B-1][0,...,L-1]. Macierz A wypełniemy zerami.

   procedure add(x){
     for i=0 to B-1 do A[i,h(i,x)]++
   }
   function count(x){
     return min{A[0,h(0,x)], A[1,h(1,x)], ... , A[B-1,h(B-1,x)]} 
   }
   

   Twierdzenie: $Pr[\mathrm{count}(x)>f_x+\frac{e}{L}f_x] \leq \left(\frac{1}{e}\right)^B$
   Dowód (hint): Stosujemy twierdzenie Markowa do zmiennej losowej $Z_x = \mathrm{count}(x) - f_x$ oraz progu $\frac{e}{L}f_x$.

05.04.2017: Streaming - II

1. Morris Probabilistic Counter
   

   C=1;
   procedure Add(){
   	if rand()<2^{-C} C++;
   }
   

   Tw: $E[2^{C_n}] = n+2$.
   Zadanie: $var[2^{C_n}] = \frac12 n(n+1)$
2. Trik medianowy.
   Twierdzenie. Niech $\varepsilon, \delta \gt 0$. Niech $X$ będzie zmienną losową o skończonym drugim momencie. Niech $K= (5 \mathrm{var}(X))/(\varepsilon^2 E(X)^2)$ oraz $L = 18\ln(1/\delta)$. Niech $(X_{ij})_{i=1\ldots L; j=1\ldots K}$ będzie rodziną niezależnych zmiennych losowych o tym samym rozkładzie co $X$. Niech $$ Y = \mathrm{median}_{i=1\ldots L}(\frac{1}{K}\sum_{j=1}^K X_{ij})~. $$ Wtedy $$ \Pr[|Y-E[X]|\geq\varepsilon E[X]) \le \delta ~. $$
3. HyperLogLog: Philippe Flajolet, Éric Fusy,Olivier Gandouet, Frédéric Meunier HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm,2007 Conference on Analysis of Algorithms, AofA 07, Juan des Pins, France, June 17-22, 2007

12.04.2017: Streaming - III

Noga Alon, Yossi Matias, Mario Szegedy, The space complexity of approximating the frequency moments

1. Dowolny moment $k\geq 2$:

   INIT: wylosuj indeks i ze zbioru {1,..n}; wyznacz a=ai; c=0;j=0;
   UPDATE(x){ j++; if ((x=a)&&(j>=i)) {c++;} }
   OUT: Z = c^k-(c-1)^k
   

   Twierdzenie: $E[Z] = \sum_a (f_a)^k$.
   Twierdzenie (bez dowodu): $var[Z] \leq k n^{1-\frac1k} E(Z)^2$.
2. Generowanie losowego elementu ze strumienia danych:

   INIT: choosen = 0; i =0
   UPDATE(x){ i++; if (random() <= 1/i) choosen=i;}
   OUT: choosen
   

   Dodów poprawności: indukcja matematyczna.
3. Konstrukcja 4-niezależnej rodziny funkcji haszujących: bierzemy ciało mocy większej niż 4. Za rodzinę funkcji haszujących bierzemy rodzinę wszystkich wielomianów stopnia $\leq$ 3. Do pokazania 4-niezalezności skorzystaliśmy ze wzoru interpolacyjnego Lagrange'a oraz z tego, że jeśli wielomian stopnia $\leq 3$ ma cztery różne pierwiastki, to jest on wielomianem zerowym.
4. Konstrukcja ciała o $2^{80}$ elementach: bierzemy wielomian nierozkładalny $w$ stopnia 80 nad ciałem $\ZZ_2$ i bierzemy ciało $\ZZ_2[x]/(w)$.
5. Drugi moment: bierzemy rodzinę 4-niezależnych funkcji haszujących H o wartościach w zbiorze $\{-1,1\}$.

   INIT: wylosuj h  <- H; c=0
   UPDATE(x){ c += h(x);}
   OUT c^2
   

   Tw. $E[c^2] = \sum_a (f_a)^2$
   Tw. $var(c^2) \leq 2 E(c^2)^2$

MAYUR DATAR, ARISTIDES GIONIS, PIOTR INDYK, AND RAJEEV MOTWANI, MAINTAINING STREAM STATISTICS OVER SLIDING WINDOWS

class SlidingWindow(N:Int,k:Int) {
	var B     = new scala.collection.mutable.ArrayBuffer[Array[Long]]()
	//* B(i)(0) = timestamp
	//* B(i)(1) = wartosc
	var LAST  : Long = 0;  //zawartosc najstarszego licznika
	var TOTAL : Long = 0;  //suma zawartosci licznikow
	var Index : Long = 0;  //liczba wczytanych liczb; czyli numer najnowszego elementu
	
	def add(x:Int):Unit = {
		Index = Index + 1;
		
		while ((B.length>0)&&(B(0)(0) < Index - N)){
			TOTAL = TOTAL - B(0)(1)
			B.remove(0);
			LAST = if (B.length>0) B(0)(1) else 0;
		}	
		if (x==1){
			B += Array(Index,1)
			TOTAL = TOTAL + 1
		}	
		var sprawdzaj = true
		while (sprawdzaj) {
			sprawdzaj = false
			var i = 0;
			...
		}
	}
	def get():Long = {TOTAL - LAST/2}
}

26.04.2017: Analiza linków

1. Pojęcie macierzy kolumnowo stochastycznej.
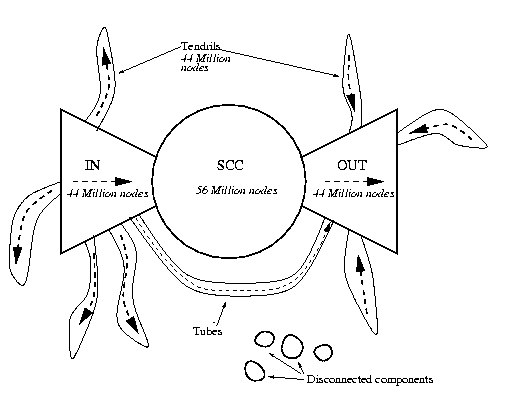
2. Struktura sieci WWW:
   
3. Macierz Google:
   $$ G_{\alpha} = \alpha\left(M + \frac1n e_A^T \cdot e\right) + \frac1n (1-\alpha)e^T\cdot e $$
   gdzie $e=(1,1\ldots,1)$ oraz $e_A=(\delta_i)_{i=1,\ldots,n}$, gdzie $\delta_i=1$ jeśli wierzchołek $i$ jest "dangling node", oraz $\delta_i=0$ w przypadku przeciwnym oraz $0 \lt \alpha\lt 1$ (Google podobno stosuje $\alpha = 0.85$).
   Źródło: Deeper Inside PageRank, Amy N. Langville and Carl D. Meyer
4. Tw. Niech $\lambda_1,\ldots\lambda_n$ będą wartościami własnymi macierzy $G\alpha$ uporządkowanymi tak aby $|\lambda_1| \geq |\lambda_2| \geq \ldots$. Wtedy
   1. $\lambda_1 = 1$ oraz $\lambda_2\leq \alpha$
   2. Jeśli graf na conajmniej dwie silne spójne składowe, to $\lambda_2 = \alpha$
   Zródło: The Second Eigenvalue of the Google Matrix, Taher H. Haveliwala and Sepandar D. Kamvar
5. PageRank: taki wektor $x = (x_1,\ldots,x_n)^T$, że $\sum_{i}x_1=1$, $(\forall i)(x_i\geq 0)$ oraz $$ G_\alpha \circ x = x ~. $$
6. Rozpisanie wzoru na rozkład stacjonarny: $$ x_i = \alpha \sum_{j} m_{ij}x_j + \alpha \frac{E_S}{n} + \frac{1-\alpha}{n} $$ gdzie $E_S = \sum_{i\in S}x_i$ zaś $S$ jest zbiorem "dangling nodes".
7. Metoda potęgowa wyznaczania PageRank: zaczynami od jakiegoś wektora probabilistycznego $X_0$ (np. $X_0=(\frac1n,\ldots,\frac1n)$), następnie iteracyjnie obliczmy $X_{n+1} = G_\alpha \circ X_n$. Z tego powodu, że $\lambda_2\leq \alpha \lt 1$ jest to proces zbieżny. Na następnym wykładzie omówimy sobie jak to możemy stosunkowo efektywnie zrobić.
8. Kod Mathematica do jednoczesnego wyznaczania i wyświetlania PageRank:

   HLG[G_,wsp_:1.0]:= Block[{rG},
     rG=PageRankCentrality[G,0.85];
     HighlightGraph[G,
       VertexList[G],
       VertexSize-> Thread[VertexList[G]->wsp*rG],
       VertexLabels->Placed["Name",Tooltip]
     ]
   ]
   

   Przykład konstrukcji grafu:

   STAR = Join[
      Table[ToString[i] -> "a", {i, 0, 9}], 
      Table[ToString[i] -> ToString[Mod[i + 1, 10]], {i, 0, 9}]
      ]; 
   

9. Bardzo prosty (tylko dla testów) spider:

   Spider[url_, dom_, k_] := Block[{G},
     IsCorrect[s_] := StringQ[s] && StringStartsQ[s, dom];
     G = NestGraph[
       Select[Import[#, "Hyperlinks"], IsCorrect[#] &] &, url, k
     ];
     Subgraph[G, Select[VertexList[G], StringQ[#] &], 
      VertexLabels -> Placed["Name", Tooltip], DirectedEdges -> True]
     ]
   

   oraz przykład jego użycia:

   MGB = Spider["http://cs.pwr.edu.pl/gebala/", "http://cs.pwr.edu.pl/gebala/", 3]
   

10.05.2017: PageRank

1. Metoda iteracyjna obliczania PageRank w technologii Map-Reduce

   Iicjalizacja

   n  = liczba stron
   Es = (liczba "wiszących stron")/n
   alfa = 0.85
   reprezentacja stron (id,1/n,L); L = lista linków z id
   

   Pętla wykonywana aż do osiągnięcia pożądanej dokładności:

   • Mapper

     INPUT: (id,v,L)
     OUTPUT:
       if (L==[]) emitt("*",v)
       else{ forall (x<-L) {emitt(x,v/length(L))}}
       emitt(id,L)
     

   • Reducer

     INPUT: (id,X)
     OUTPUT:
       L = lista z X;
       Y = liczby z X;
       s = suma liczb z Y
       if (id=="*") {E= s}
       if (id!="*"){
     	  v = alfa(s+Es/n)+(1-alfa)/n;
     	  emitt(id,v,L)
       }
     

   • FINALLY

       Es = E
     

2. Metoda oparta na podziale macierzy Googla na bloki. Podstawa teoretyczna: $$ M_{n\times n}(M_{k\times k}(R)) \sim M_{(nk)\times (nk)}(R) $$ gdzie $R$ jest dowolnym pierścieniem przemiennym.
3. "Energia" zbioru linków $X$ : $E_X = \sum\{\pi_i:i\in X\}$
4. Równanie SEO $$ E_X = \frac{\alpha}{1-\alpha}\left(E_1+E_2 \frac{|X|}{n}\right) +\frac{|X|}{n} - \frac{\alpha}{1-\alpha}(E^{out}+E^{sinks}) $$ gdzie
   1. $E_1$ = energia otrzymywana z zewnątrz: $E_1 = \sum_{x\in X}\sum_{y\notin X}p_{x,y}\pi_y$
   2. $E_2$ = energia wszystkich sinków: $E_2 = \sum\{\pi_i:i \mbox{ jest sinkiem}\}$
   3. $E^{out}$ = energia przekazywana z $X$ do otoczenia
   4. $E^{sinks}$ =energia sinków z $X$
5. Pojęcie "Link Farm"
6. Wykrywanie link spam: Discovering Large Dense Subgraphs in Massive Graphs, David Gibson Ravi Kumar Andrew Tomkins
7. Nowoczesne algorytmy Googla:
   1. 2011: Panda (analiza treści; np. wyszukiwanie plagiatów)
   2. 2011: Pingwin (analiza nienaturalnych linków)
   3. 2012: Koliber (elementy semantyki)
   4. 2012: Gołąb (lokalizacja przestrzenna wyników)

17.05.2017: Reguły asocjacyjne

1. Fakt: Jeśli $\pi_1,\ldots,\pi_n$ są wektorami probabilistycznymi, $\sum_i a_1 =1$, $a_1, \ldots, a_n \geq 0$, to $\sum_i a_i \pi_i$ jest również wektorem probabilistycznym
2. Twierdzenie Arrowa
3. Ustalamy $I$ - zbiór itemów; transakcją nazywamy podzbiór $I$; ustalamy ciąg (transakcji) $T = (t_i)_{i=1,\ldots, n}$.
   1. Nakryciem (cover) zbioru $X\subseteq I$ nazywamy zbiór $cov(X) = \{i: X \subseteq t_i\}$
   2. Supportem zbioru $X\subseteq I$ nazywamy liczbę $s(X) = |cov(X)|$
   3. Regułą asocjacyjną nazywamy parę niepustych rozłącznych podzbiorów $X,Y \subseteq I$ zapisywaną jako $X\Rightarrow Y$
   4. Współczynnik wiarygodności (confidence): $c(X\Rightarrow Y) = \frac{s(X\cup Y)}{s(X)}$
   5. Współczynnik ciekawości reguły: $I(X\Rightarrow Y) = c(X\Rightarrow Y) \frac{n}{s(Y)}$
   6. Przykłady:
      • {Pieluszki} $\Rightarrow$ {Piwo} (przypuszczalnie "Urban Legend")
      • {Huragan} $\Rightarrow$ {Strawberry pop tart} (sic!!!)
   7. CEL: mamy ustalony parametr $s_{min}$ oraz $c_{min}$; chcemy wyznaczyć wszystkie reguły $X\Rightarrow Y$ takie, że $s(X\cup Y) \geq s_{min}\cdot n$ oraz $c(X\Rightarrow Y) \geq c_{min}$.
   8. Fakt (antymonotoniczność)$X\subseteq Y \subseteq I \to s(X)\geq s(Y)$
   9. Wniosek (Reguła Apriori): Jeśli $s(X) \lt s_{min}\cdot n$ i $X\subseteq Y$, to $s(Y) \lt s_{min}\cdot n$
      Interpretacja: jeśli $X$ nie jest interesujący, to również dowolny jego nadzbiór nie jest interesujący.
   10. Schemat algorytmu Apriori (Agrawal, 1993)

       k=1
       F1 = czeste itemy
       repeat
         k++
         C(k) = kandydaci (zbiory k elementowe) zbudowani z F(k-1)
         forall (t <- T) {
           forall (c <- C(k)){
       	  if (c jest podzbiorem t)
               sigma(t)++
       	}
         }
         F(k) = {c: sigma(c) >= smin*n}
       until (F(k)=0)
       F = suma F(k)
       

       Sposób budowania zbioru kandydatów - następny wykład.

24.05.2017: Reguły asocjacyjne - II

1. Detale implementacyjne programu Apriori
   1. Pierwszy przebieg: wyznaczamy częste single i od tej pory posługujemy się tylko częstymi singlami
   2. Numeracja par: $f(i,j) = (i-1)(n - i/2)+ (j-i)$
   3. Tablica haszująca
   4. Metody $F_{k+1} = F_{k}\star F_1$, $F_{k+1} = F_{k}\star F_k$
   5. Metoda wyznaczania reguł z częstych zbiorów.
2. Algorytm PCY: haszujemy pary w pierwszym przebegu
3. Algorytm Apriori Christiana Borgelt'a

31.05.2017: Klasteryzacja - I

1. Podział algorytmów klasteryzacyjnych: hierarchiczne/"przypisania punktów", euklidesowe/nieeuklidesowe, małe/duże
2. Sfera nie jest płaska: nie istnieje izometryczne zanurzenie sfery w przestrzeń $\RR^n$
3. "Klątwa wymiarowości":
   1. Kod programu Mathematica służący do wyznaczanie histogramu odległości miedzy losowymi punktami $[0,1]^{dim}$:

       
      SDH[dim_,sample_]:= Histogram[
        Map[Norm, 
          RandomReal[1, {sample,dim}] - RandomReal[1,{sample,dim}]
        ] / Sqrt[dim], 
        {0,1,0.025}
      ]
      

   2. Fakt: Jeśli $X_n, Y_n$ są losowymi punktami $[0,1]^n$ to $\lim_n \frac{E[|X_n-Y_n|]}{\sqrt{n}} = \sqrt{\frac16}$.
   3. Kod programu Mathematica służący do wyznaczanie histogramu iloczynu skalarnego losowych wektorów z $[-1,1]^{dim}$:

       
      IPH[dim_, sample_] := Block[{
         X = Map[Normalize, RandomReal[{-1, 1}, {sample, dim}]],
         Y = Map[Normalize, RandomReal[{-1, 1}, {sample, dim}]],
         Z = Table[0, sample],
         i},
        For[i = 1, i <= sample, i++,
         Z[[i]] = (X[[i]].Y[[i]]);
         ];
        Histogram[Z]
        ]
      

      Wniosek: wraz ze wzrostem wymiarów wzrasta prawdopodobieństwo tego, że dwa losowe wektory są ortogonalne.
   4. Wzór na objętość kuli w przestrzeni $\RR^n$: $$ vol(K(0,r)) = \frac{\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2}+1)} \cdot r^n $$

07.06.2017: Klasteryzacja - II

1. Sortowanie dużych zbiorów: tniemy na części, któe mieszczą sie w pamięci; sortujemy te części w pamięci; zapisujemy na dysku/dyskach; następnie stosujemy scalanie; schemat scalania: drzewo $k$-arne (szczegóły: D. Knuth: Sztuka Programowania, vol. III, hasło: sortowanie zewnętrzne)
   Przyśpieszenie: buforujemy scalane pliki; rozmiar buforów - możliwie duży (nie korzystamy z buforowania systemowego).
2. Algorytmy hierarchiczne: różne sposoby reprezentacji klastrów; organizacja pamieci
3. Algorytm k-Means
4. Implementacja algorytmu k-Means w środowisku Map-Reduce
5. Podział otrzymany algorytmem kMeans dla k=1,2,...,9 na losowych danych z kwadratu
   
6. Zastosowanie algorytmu kMeans do wyróżnienia szczgółów morfologicnych tomografu głowy:
   
7. Słabe punkty algorytmu k-Means: dwa koncentryczne zbiory punktów (liczba klastrów: 2):
   
   Możliwe rozwiązanie problemu: podwyższenie wymiaru $$ f:\RR^2 \to \RR^3: (x,y) \to (x,y,C(x^2+y^2)) $$
8. Algorytm DBScan: punkty wewnętrzne, punkty brzegowe, outliners.
9. Problem zaginionej krowy McDonaldsa
10. "Ski rental problem"

14.06.2017: Redukcja wymiarów

1. Macierze ortogonalne: $U\cdot U^T = I$
   1. $U\cdot U^T = I \to det(U)\in \{-1,1\}$
   2. $U\cdot U^T = I \to U^{-1} = U^T$
   3. $U\cdot U^T = I \equiv (\forall x,y) ((Ux)^T\cdot Uy = x^T \cdot y)$
2. Macierze symetryczne: $A = A^T$
   1. Jeśli $A = A^T$, $x,y\neq 0$, $Ax=\lambda x$, $Ay = \nu y$ oraz $\lambda\neq \nu$, to $x^T y = 0$
   2. Jeśli $A = A^T$, $x\neq 0$, $Ax=\lambda x$ to $\lambda\in \RR$
   3. Jeśli $A = A^T$, $Ax=\lambda x$ i $x^Ty=0$, to $x^T(Ay) = 0$
   4. Macierz $A$ jest symetryczna wtedy i tylko wtedy, gdy $(\forall x,y)\left((Ax)^Ty = x^T Ay\right)$
   5. WNIOSEK: Jeśli $A = A^T$, to istnieje macierz ortogonalna $U$ oraz macierz diagonalna $\Sigma$ taka, że
      $$ A = U\cdot \Sigma \cdot U^T $$
3. Metoda PCA
   1. Mamy macierz $X_0$ wymiaru $n\times p$. Liczbę $p$ interpretujemy jako liczbę zmiennych, $n$ jako liczbę pomiarów
   2. Porządkujemy macierz: kolumny mają mieć średnią zero i wariancję 1. Otrzymujemy macierz $X$.
   3. Do macierzy $X^T\cdot X$ stosujemy twierdzenie o postaci macierzy symetrycznych. Znajdujemy macierz uniterną $U$ i diagonalną $\Sigma$ takie, że $$X^T X = U \Sigma U^T$$ Możemy założyć, że na przekątnej macierzy $\Sigma$ występują wartości własne w kolejności $\lambda_1 \geq \lambda_2 \geq \ldots \geq \lambda_n \geq 0$.
      Uwaga: to, że wartości własne są nieujemne wymaga sprawdzenia: oblicz $||Xu||^2$ dla wektora własnego $u$ maierzy $X^TX$.
   4. Bierzemy kilka pierwszych kolumn $u_1,\ldots u_k$ macierzy ($k\leq p$) i przekształcamy macierzy $X$: $X\cdot[u_1,\ldots,u_k]$. Typowy wybór: tak wybieramy $k$ aby $\sum_{i=1}^{k} \lambda_i \geq 0.9 \sum_{i=1}^{n} \lambda_i$ (ale to trzeba sprawdzić eksperymentalnie).
   5. Zastosowanie metody PCA dla klasycznego przykładu IRIS.DAT (p=4;n=150; k=2):
      
   6. Wyjaśnienie metody: chcemy zoptymalizować funkcję $f(u) = (Xu)^T\cdot Xu$ na zbiorze tych $u$, że $||u||=1$. Korzystamy z metody mnożników Lagrange'a. Stwierdzamy (dosyć proste obliczenia), że ekstrema są przyjmowane w wektorach własnych macierzy $X$.
4. Rozkład SVD
   1. Bierzemy dowolną macierz $A$ o wymiarach $n\times p$. Tworzymy z niej macierz $B=A^TA$. To jest macierz symetryczna o wymiarach $p\times p$. Stosujemy do niej twierdzenie o rozkładzie dla macierzy symetrycznych. Znajdujemy macierz ortogonalną $V$ oraz diagonalną $\Sigma$ taką, że $$ A^TA = V\cdot\Sigma\cdot V^T. $$
   2. Kolumny macierzy $V$ tworzą bazę ortonormalną $\{v_1,\ldots,v_p\}$. Są one wektorami własnymi macierzy $A^TA$. Niech $ (A^TA)v_i = \lambda_i v_i$. Wiemy, że wartości własne są nieujemne. Porządkujemy je tak aby $$ \lambda_1 \geq \lambda_2 \geq \ldots \geq \lambda_k \gt \lambda_{k+1} = \ldots = \lambda_p = 0~. $$
   3. Sprawdzamy, że $||AV_i|| = \sqrt{\lambda_i}$ (Wskazówka 1: łatwe; Wskazówka 2: zacznij liczyć $||Av_i||^2$)
   4. Wiemy, że $(Av_i)^T (A v_j) = 0$ dla $1\leq i \lt j\leq p$. Wektory $$ Av_1, \ldots Av_k $$ są niezerowe i ortogonalne. Normujemy je, czyli kładziemy $u_i = Av_i/\sqrt{\lambda_i}$. Teraz wektory $u_1,\ldots,u_k$ są ortogonalne i mają długość 1. Rozszerzamy ten układ wektorów do bazy $u_1,\ldots,u_n$ ortonormalnej przestrzeni $\RR^n$.
   5. Z wektorów $u_1,\ldots,u_n$ budujemy (ustawiając je w kolumny) drugą macierz ortogonalną $U$.
   6. Z pierwiastków wartości własnych $\sqrt{\lambda_1},\ldots,\sqrt{\lambda_p}$ budujemy macierz przekątniową $\Sigma$ o wymiarach $n\times p$. Sprawdzamy, że $$ U \cdot \Sigma = A \cdot V~. $$
   7. Mnożąc obie strony przez $V^T$ otrzymujemy następujący rozkład macierzy $A$:
      $$ A = U \cdot \Sigma \cdot V^T $$
      To jest właśnie rozkład SVD macierzy $A$ !!!
   8. Wizualizacja dla macierzy $3\times 2$ $$ \begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\\a_{31}&a_{32}\end{bmatrix} = \begin{bmatrix}u_{11}&u_{12}&u_{13}\\u_{21}&u_{22}&u_{23}\\u_{31}&u_{32}&u_{33}\end{bmatrix} \cdot \begin{bmatrix}\sqrt{\lambda_1}&0\\0&\sqrt{\lambda_2}\\0&0\end{bmatrix} \cdot \begin{bmatrix}v_{11}&v_{12}\\v_{21}&v_{22}\end{bmatrix}^T $$
   9. A na konice zrobiliśmy sobie zdjęcie (niezbyt dobrze wyszło) i zastosowaliśmy rozkład SVD do jego kompresji. Okazało się, że biorąc 50 z 720 wektorów własnych potrafimy całkiem dobrze odtworzyć oryginalne zdjęcie.