Zadania 1 i 2

W niniejszym zadaniu ulepszony został algorytm rozproszony, w oparciu o który stacje uzyskują dostęp do kanału radiowego. Przy pomocy modelu matematycznego oraz wyników symulacji wykazana została poprawa jakości wykorzystania dostępnego pasma radiowego w stosunku do obecnie znanych metod. W przypadku transmisji bezprzewodowych zasadnym jest rozważanie modelu, w którym brak jest zewnętrznego mechanizmu koordynującego wykorzystanie kanału radiowego. Stosowane algorytmy dostępu do kanału (ang. MAC - medium access control) mają za zadanie określenie momentu nadawania dla stacji jedynie na podstawie bieżącego stanu kanału. Problem ten był rozwiązywany w różny sposób. Chronologicznie pierwszym rozwiązaniem był protokół ALOHA oraz jego wersja synchroniczna - slotted ALOHA. W pracy skoncentrowano się na metodach opartych na wykrywaniu fali nośnej (ang. carrier sensing - CS). Wszystkie mechanizmy CSMA (ang. carrier sense multiple access - dostęp dla wielu stacji poprzez wykrywanie nośnej) zakładają, że stacja przed wysłaniem wiadomości nasłuchuje przez krótki okres, by sprawdzić czy nie trwa właśnie inna transmisja. Samo sprawdzanie może opierać się o fizyczne właściwości medium (np. pomiar poziomu sygnału względem ustalonego poziomu szumów), bądź też wykorzystywać wyższe warstwy protokołu komunikacyjnego - np. poszukiwanie preambuły wiadomości, poprzedzającej każdą transmisję. Drugim elementem różniącym protokoły tej rodziny jest sposób, w jaki stacja postępuje po zbadaniu stanu kanału:

• nieciągłe CSMA w przypadku wykrycia wolnego kanału stacja transmituje; w przypadku zajętego – stacja ponawia próbę po ustalonym czasie (ang. back-off time);
• p-ciągłe CSMA w przypadku wolnego kanału stacja rozpoczyna transmisję z prawdopodobieństwem $p$, zaś z prawdopodobieństwem $(1-p)$ ponawia próbę po ustalonym czasie $\alpha$; w przypadku zajętego kanału stacja aktywnie czeka na zakończenie transmisji i rozpoczyna procedurę jak w przypadku wolnego kanału. Istotnym przypadkiem $p$-ciągłego CSMA jest $p=1$, w którym stacja aktywnie czeka na koniec innej transmisji by bezwarunkowo rozpocząć swoją. Stąd, gdy podczas pewnej transmisji dwie inne stacje rozpoczną wykonywanie protokołu, z pewnością nastąpi kolizja. Koniec poprzedniej transmisji daje możliwość tymczasowej synchronizacji stacji, a wprowadzenie $p<1$ umożliwia rozładowanie ruchu nagromadzonego w trakcie trwania poprzedniej transmisji. W niniejszej pracy korzystano z tych dwóch obserwacji i pokazano rozkład dla p poprawiający przepustowość sieci poprzez zredukowanie prawdopodobieństwa niepowodzenia synchronizacji.

W tej części pracy zaprezentowany został nowy protokół $\lambda$-ciągły dostępu do kanału radiowego bazujący na algorytmach wyboru lidera. Algorytm ten wykorzystuje standardowe mechanizmy CS oraz poprawia p-ciągły CSMA.

Protokół z wykorzystaniem stałego opóźnienia i optymalnego rozkładu niejednostajnego

W protokole tym podobnie jak w klasycznym p-ciągłym CSMA, stacje czekają do momentu kiedy kanał radiowy jest wolny. Wtedy, zamiast nadawać ze stałym prawdopodobieństwem $p$ i odczekać okres $\lambda$ do następnej próby, wykorzystują kilka punktów transmisji z różnymi prawdopodobieństwami. Niech $N$ oznacza liczbę stacji starających się o dostęp do kanału radiowego. Dwa punkty transmisji: W tym szczególnym przypadku po zwolnieniu kanału radiowego stacje decydują niezależnie czy mają nadawać od razu czy po odczekaniu czasu $\lambda$ czy może w ogóle wstrzymać się z transmisją. Niech $p\in [0,1]$ oznacza prawdopodobieństwo, że stacja rozpoczyna transmisję od razu i $q\in [0,1]$ prawdopodobieństwo, że dopiero po odczekaniu czasu $\lambda$ oraz załóżmy, że $p+q \leqslant 1$. Tym samym z prawdopodobieństwem $1 - (p+q)$ stacja wstrzymuje się z transmisją. Prawdopodobieństwo nadawania dokładnie jednej stacji w tym modelu zależy od parametrów $N$, $p$ oraz $q$ i wynosi \begin{equation} \label{eqn:prsuc} Pr[Success] = N p(1-p)^{N-1} + N q (1-(p+q))^{N-1} \end{equation} W tym szczególnym przypadku można znaleźć dokładne wzory na prawdopodobieństwa $p$ i $q$, które maksymalizują sukces protokołu. Mianowicie, niech \begin{equation*} f(p,q) = N p(1-p)^{N-1} + N q (1-(p+q))^{N-1} \end{equation*} Przy pomocy standardowych narzędzi Analizy Matematycznej można pokazać, że funkcja osiąga maksimum dokładnie dla \begin{equation*} p = 1-q N \mbox{ oraz } q = \frac{(N-1)^2}{N^2(N-1-(\frac{N-1}{N})^N)}~. \end{equation*} Ze wzorów tych wynika, że dla dużych $N$, $q=1/N + O(1/N^2)$ oraz $p=(1-1/e)/N + O(1/N^2)$, czyli $p \approx 0.632/N$. Podstawiając tak wyznaczone parametry $p$ i $q$ do wzoru dla $N=1,\ldots,10$ otrzymano następujące prawdopodobieństwa sukcesu $0,666667$, $0,612476$, $0,589383$, $0,576551$, $0,568379$, $0,562717$, $0,558561$, $0,555382$, $0,55287$. Ogólny przypadek: Dla $k\geqslant 1$ punktów transmisji (tj. nadawanie może rozpocząć się w momentach $0, \lambda, \ldots, (k-1)\lambda$ założono, że prawdopodobieństwa wyboru przez każdą stację $i$-tego momentu transmisji (każda stacja wybiera co najwyżej jeden moment) wynosi $p_i$ , gdzie $p_1,p_2,\ldots,p_k \leqslant 1$ są dodatnimi liczbami rzeczywistymi takimi, że $p_1 + \ldots + p_k \leqslant 1$. Wtedy prawdopodobieństwo tego, że dokładnie jedna stacja rozpocznie nadawanie między $0$ a $(k-1)\lambda$ wynosi \begin{equation} \label{eqn:prsucgeneral} \Pr[Sukces_{p_1,\ldots,p_k}] = \sum_{i=1}^k N p_i (1-(p_1 + \ldots + p_i))^{N-1}, \end{equation} a całkowity czas wysłania pakietu wraz z czasem przeznaczonym na losowanie to $T_k = k\cdot \lambda + \delta$, gdzie $\delta$ to czas wysyłania jednego pakietu. Precyzyjne wzory analityczne na prawdopodobieństwa $p_1, p_2, \ldots, p_k$ optymalizujące prawdopodobieństwo są trudne do wyznaczenia. Zakładając jednak, że możemy posłużyć się pewnym przybliżeniem. Otóż oznaczając $p_i = a_i/N$ posłużyć się można przybliżeniem $1-(p_1 + \ldots + p_i) \approx e^{-(a_1 + a_2 + \ldots a_i)}$ i zagadnienie optymalizacji prawdopodobieństwa sprowadza się do maksymalizacji następującej funkcji: \begin{equation*} f_k(a_1,\ldots,a_k) = \sum_{i=1}^k a_i e^{-(a_1 + \ldots + a_i)}~. \end{equation*} Niech $(M_k)_{k\geqslant 1}$ będzie ciągiem liczb rzeczywistych zdefiniowany następującą relacją rekurencyjną: \begin{equation*} \left\{ \begin{array}{lcl} M_1 & = & 1/e \\ M_{k+1} & = & e^{-1+M_k} \mbox{ dla } k\geqslant 1 \end{array} \right. \end{equation*} Można pokazać, że optymalne rozwiązania wyrażają się za pomocą tych liczb:

Lemat 1: Funkcja $f_k$ osiąga maksimum dla $(b_k,\ldots,b_1)$ , gdzie $b_1=1$ i $b_a = 1-M_{a-1}$ dla $a=2,\ldots,k$ oraz maksimum to wynosi $M_k$.

Implementacja

Zadaniem powyższego algorytmu opracowanego przez Politechnikę Wrocławską, a zaimplementowanego przez Datax jest zapewnienie przydziału do kanału radiowego współdzielonego przez wiele węzłów dla nadawcy zgłaszającego potrzebę transmisji. Żaden z węzłów w sieci nie ma nadrzędnej roli nad pozostałymi. Główne etapy prac w zad. 2 wymienione są poniżej

1. Implementacja algorytmu przydziału do kanału: Algorytm został zaimplementowany w sieci tworzonej w ramach toczącego się przez cały projekt zad. 13. Opracowane zostały zasady interakcji pomiędzy różnymi warstwami węzłów w zależności od zadanych parametrów, takich jak liczba węzłów N oraz liczba punktów transmisji k.
2. Przeprowadzenie symulacji i opracowanie wyników: Symulacje mają na celu weryfikację podstawowych założeń zaproponowanego protokołu, dlatego też nie zostały uwzględnione zjawiska fizyczne związane z propagacją fal radiowych (opóźnienie, tłumienie). Symulacja zakłada, że wszystkie stacje znajdują się w swoim wzajemnym zasięgu i przypadku jednoczesnej transmisji pakietu przez dwa węzły powstaje kolizja. W celu lepszego zrozumienia i łatwiejszej analizy zachowania algorytmu powstała funkcjonalność przedstawiająca zachowanie się węzłów w czasie. Przykładowy zapis przebiegu fragmentu symulacji zaprezentowany jest poniżej:
   

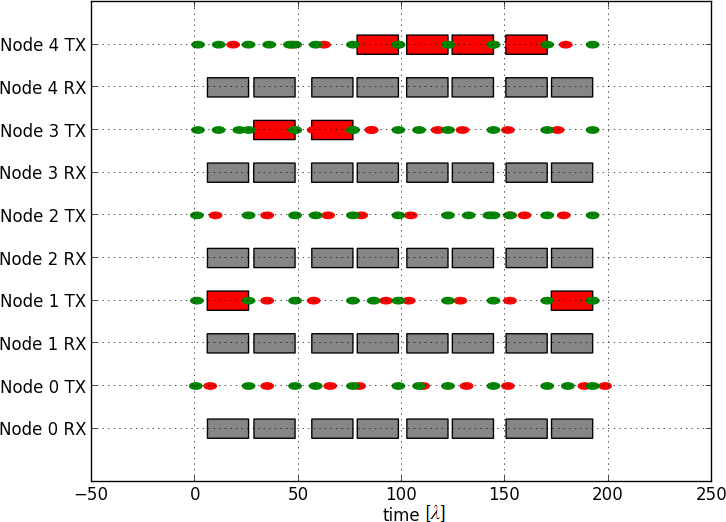
   Przebieg czasowy pojedynczej symulacji dla $N = 5$, $k =1$, $\delta = 20 \lambda$, dla modelu danych FB.
   $\blacksquare$ - okresy nadawania, $\blacksquare$ - czas kiedy można wykryć nośną, $\bullet$ - losowanie punktu transmisji, $\bullet$ – wykryto inną nadającą stację

3. Zestawienie wyników teoretycznych z wynikami symulacji: Przedstawiona metoda uzyskiwania dostępu do kanału radiowego wykazuje lepsze własności niż proste rozwiązania rozważane wcześniej (np. metoda odpowiadająca przypadkowi k = 1). Asymptotyczne własności protokołu zostały potwierdzenie przez symulacje. Prawdopodobieństwa przesłania pakietów bez kolizji Mk pokrywają się z wartościami Pk wyznaczonymi eksperymentalnie.
   

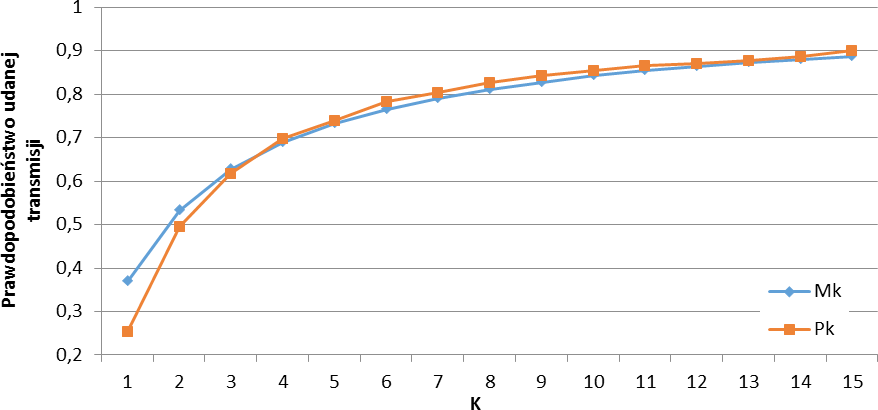
   Prawdopodobieństwo udanej transmisji wyznaczone teoretycznie(Mk) oraz eksperymentalnie (Pk)

   Symulacje wykazują, że wraz ze wzrostem $k$, system osiąga coraz większą przepustowość (poprawa o 50\% dla $k = 15$ w porównaniu z p-ciągłym CSMA, a więc gdy $k = 1$).
   

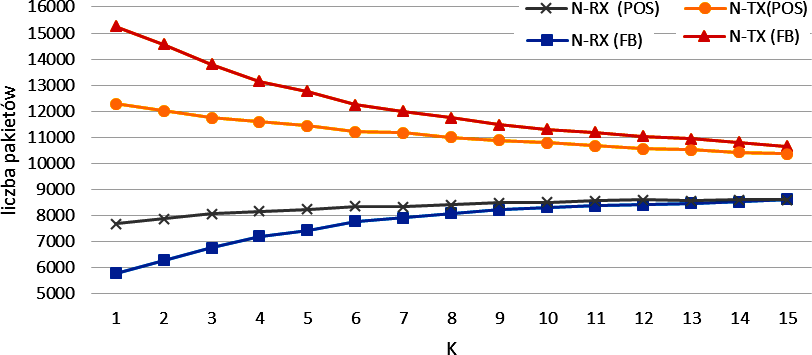
   Liczba pakietów odebranych (N-RX) oraz nadanych (N-TX) w symulacjach z użyciem ciągłej generacji pakietów (FB) oraz generacji pakietów zgodnej z rozkładem Poissona (POS)}

   Poprawa przepustowości odbywa się kosztem mniejszej zajętości kanału i dłuższego oczekiwania pakietów w buforze.
   

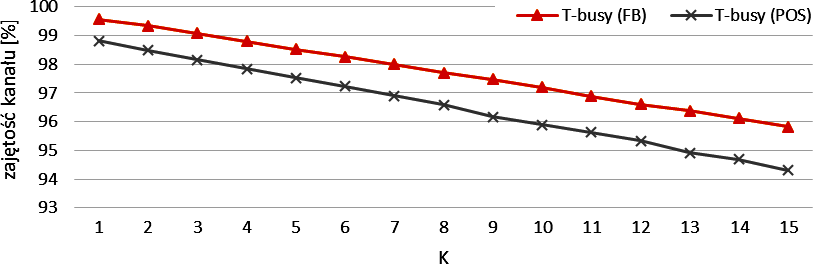
   Czas zajętości kanału (T-busy) w symulacjach z użyciem ciągłej generacji pakietów (FB) oraz generacji pakietów zgodnej z rozkładem Poissona (POS)}

   

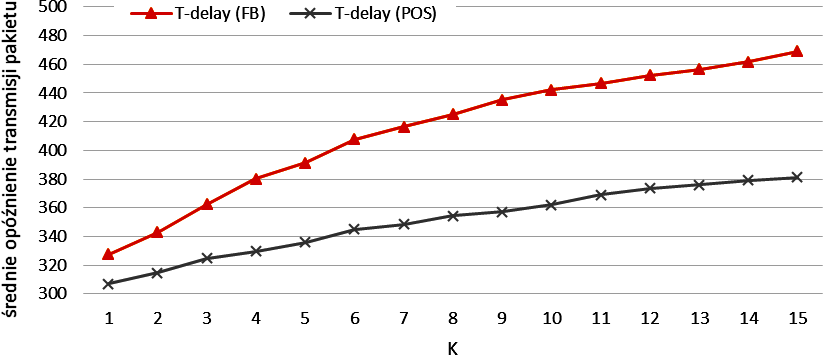
   Średnie opóźnienie transmisji pakietu (T-delay) w symulacjach z użyciem ciągłej generacji pakietów (FB) oraz generacji pakietów zgodnej z rozkładem Poissona (POS)

   Wydłużenie opóźnienia transmisji nie jest jednak problemem z punktu widzenia wyższych warstw stosu protokołów, ponieważ ich wydajność zależy głównie od czasu potrzebnego na przesłanie pakietów bez kolizji.