ODOKRIM

Jedną z informacji mających kluczowe znaczenie w procesie inicjalizacji sieci single-hop jest rozmiar tej sieci. Znajomość rozmiaru sieci lub jego dobrego przybliżenia istotnie wpływa na wydajność rozważanych przez nas algorytmów inicjalizacji. W ramach Zadania 3 zaproponowaliśmy nowy algorytm przybliżonego zliczania liczby stacji w sieci single-hop, który jest łatwiejszy w implementacji i bardziej efektywny od dotychczas proponowanych rozwiązań. Proponowany algorytm opiera się na mechanizmie wykrywania fali nośnej, a jego główną zaletą jest to, że nie wymaga precyzyjnej synchronizacji zegarów stacji. Zaleta ta istotnie odróżnia nowe rozwiązanie od wcześniejszych, w których dostęp do kanału komunikacyjnego był najczęściej oparty na wielodostępie z podziałem czasowym (ang. TDMA). Rozwiązania oparta na TDMA wymagają synchronizacji wszystkich urządzeń w sieci, co jest zadaniem nietrywialnym i wymagającym odrębnej procedury. Punktem wyjścia dla zaproponowanego przez nas algorytmu przybliżonego zliczania jest następujący proces: $n$ łuków $A_1, A_2, \ldots, A_n$, każdy długości $\alpha<1$ jest losowo rozmieszczanych na obwodzie $K$ okręgu o długości $1$. Pozycje łuków są wybierane niezależnie i jednostajnie. Zajęta część obwodu $A$ możemy wyrazić jako sumę zbiorów $A=\bigcup_{i=1}^n A_i$. Dla $\mu$ oznaczającego miarę Lebesgue’a na $K$ definiujemy zmienną losową \begin{equation*} S = 1 - \mu(A) \end{equation*} oznaczającą całkowitą długość części obwodu, która nie została pokryta przez żaden łuk. Można pokazać, że \begin{equation*} E[S] = \int_K Pr[x \notin A] d\mu(x) = (1-a)^n~. \end{equation*} Kluczowa obserwacja to, że jeśli początkowa liczba łuków $n$ jest nieznana, można uzyskać jej dobre przybliżenie na podstawie wartości przyjętej przez zmienną losową $S$. Estymator parametru $n$ można wyprowadzić np. metodą momentów: \begin{equation*} \hat{n} = \ln S / \ln(1-a)~. \end{equation*} W oparciu o przedstawiony proces zaprojektowaliśmy rozproszony algorytm estymacji liczby stacji w sieci single-hop (rys. 1). Algorytm jest wykonywany jednokrotnie w wybranym momencie $t_0$ ale wskazania zegarów poszczególnych stacji mogą się od siebie różnić. Każda stacja losuje liczbę $\xi \in [0,1]$ i w momencie $t_0$ czeka przez czas długości $\xi$. Następnie stacja wykonuje przez $k\geqslant 3$ rund następującą procedurę. W rundzie $i$ wysyła sygnał długości $a$, słucha przez czas $1-a$ i zwraca całkowity czas $S_i$ kiedy kanał nie był zajęty przez żadną stacje (ang. idle). Ostatecznie algorytm zwraca estymację opartą o najmniejszą spośród wartości $S_i$.

  Algorytm 1 EstymacjaRozmiaru$(t_0, \alpha, k)$

    Inicjalizacja:
      $\xi \gets losowaLiczba([0,1])$
    
    W chwili $t_0$ zgodnie z moim zegarem:
      czekaj przez czas $x_i$
      for $i=1,2,\ldots,k$
        nadaj sygnał długości $a$
        słuchaj kanał przez czas $1-a$
        $S_i \gets$ całkowity czas ciszy w tej rundzie
    $S \gets \min\{S_1,S_2,\ldots,S_k\}$
    return $\hat{n} \gets \ln(S) / \ln(1-a)$

Poprawność opisanego algorytmu opiera się na poniższym twierdzeniu, którego prawdziwość została dowiedziona.

Twierdzenie 1 Załóżmy, że Algorytm 1 jest uruchamiany z parametrem $k\geqslant 3$ oraz, że $\Delta t \leqslant k-2$ będzie największą różnicą we wskazaniach zegarów (po wszystkich parach stacji). Wówczas dla dowolnie wybranego urządzenia $D$ istnieje $i\in \{1,2,\ldots,k\}$ takie, że każde urządzenie nadaje w te $i$-tej rundzie urządzenia $D$ przez czas $a$ oraz zachodzi relacja $S_i = \min\{ S_1, S_2, \ldots, S_n \}$.

Zbadaliśmy również właściwości wykorzystywanego w algorytmie estymatora. Wyniki są zawarte w następujących twierdzeniach.

Twierdzenie 2 Jeśli $a \leqslant 1/n$ to wartość oczekiwana estymatora $\hat{n} = \ln(S)/\ln(1-a)$ wyraża się wzorem \begin{equation*} E[\hat{n}] = (n-1) - \frac12 a(n-1)\frac{e^{an}-1}{an}+O\bigl(\frac1n\bigr) \end{equation*}

Twierdzenie 3 Jeśli $a \leqslant 1/n$ to wariancja estymatora $\hat{n} = \ln(S) / \ln(1-a)$ wyraża się wzorem \begin{equation*} Var[\hat{n}] = 2\sigma_3(an)an^2 + (1-3\sigma_1(an))an + 4\sigma_1^2(an) + 4\sigma_2(an) - 6\sigma_1(an) + o(an)~. \end{equation*} gdzie \begin{equation*} \sigma_1(x) = \frac{e^x-1}{x}, \quad \sigma_2(x) = \frac{e^x-1-x}{x^2}, \quad \sigma_3(x) = \frac{e^x-1-x-x^2/2}{x^3}~. \end{equation*}

Z Twierdzenia 3 można wydedukować, iż dla $a \leqslant 1/n$ mamy $Var[\hat{n}] = O(an^2)$. Rozpatrywany estymator jest zatem dobrze skoncentrowany (porównaj: Rys. 2).

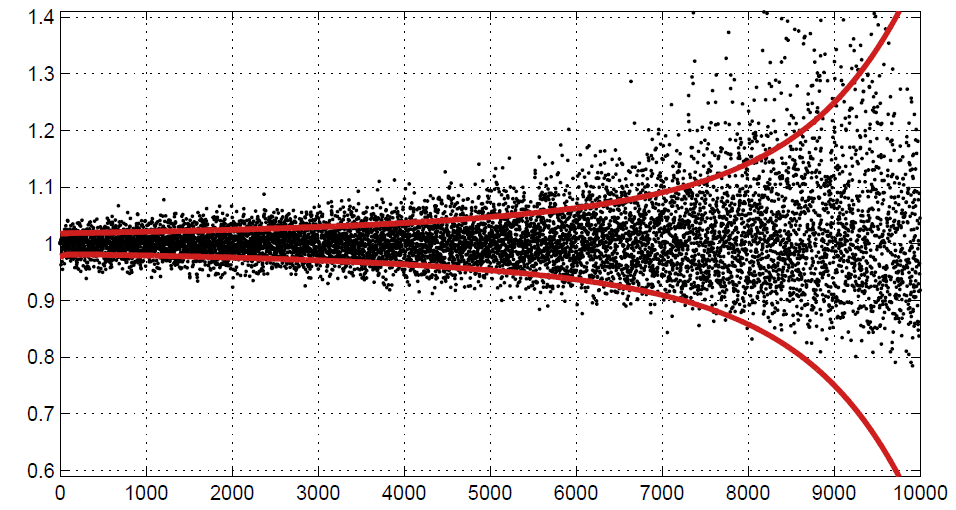
Wykres przedstawia wartości $\hat{n}/n$ (kropki) dla $n=1, \ldots, 10000$ oraz $a=1/1000$. Linie ciągłe przedstawiają wartości funkcji $1 \mp \sqrt{Var[\hat{n}]/n}$. Wykres sugeruje, że estymator jest silnie skoncentrowany również poza zakresem objętym formalną analizą

Implementacja

Rozważania teoretyczne oraz analiza wyników zadania drugiego pokazały, że jednym z najistotniejszych elementów podczas inicjalizacji grupy w sieci single-hop jest zliczenie węzłów należących do tej grupy. Wyzwaniem jest fakt, iż węzły nie mają idealnie zsynchronizowanych zegarów oraz na ich działanie wpływa również środowisko zewnętrzne zachowujące się w sposób nieprzewidywalny. W związku z tym najważniejsze kroki podczas realizacji zadania czwartego to:

Konfiguracja stworzonej w zad. 13 sieci bezprzewodowej umożliwiające zasymulowanie działania w rzeczywistych warunkach interferencyjnych Sieć zaimplementowana w zad. 13 posiada zamodelowane najważniejsze zjawiska dotyczące sieci radiowych takie jak straty propagacyjne sygnału, zaniki szybkie, zaniki wolne czy zakłócenia (interferencje). Dodatkowo modelowane są parametry węzłów takie jak czułość odbiornika czy moc nadajnika. Aby przybliżyć model sieci do rzeczywistych warunków interferencyjnych zaproponowany został poniższy model rozmieszczenia węzłów. Stacje nadawcze rozmieszczono w kwadracie o boku 100 metrów, co ma odpowiadać np. hali w fabryce. Obszar ten jest zaznaczony jako „A” na poniższym schemacie:

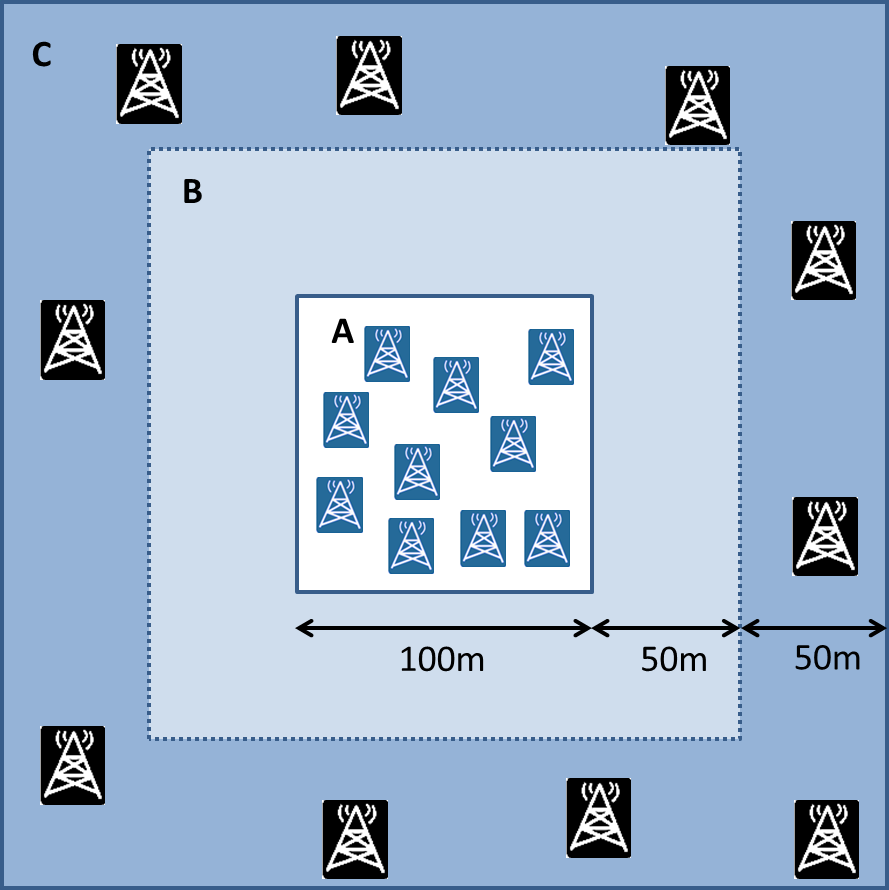
Schemat rozmieszczenia użytkowników z zaznaczonymi obszarami

Węzły w wewnętrznym kwadracie (obszar „A”) są to węzły, które biorą udział w algorytmie zliczania – wysyłają i odbierają sygnały. Węzły w obszarze „C” jedynie wysyłają sygnały, same nie uczestnicząc w procesie zliczania. Ich zadaniem jest wprowadzenie zakłóceń do obszaru A. Obszar „B” jest strefą buforową – nie mogą się w niej znajdować żadne węzły. Między obszarami A i B założono istnienie ściany. Tak więc zmieniając liczbę węzłów w obszarze C można zasymulować różne poziomy interferencji zewnętrznych.
Analiza wyników symulacji, w szczególności sugestia dotycząca parametrów konfiguracyjnych algorytmu w zależności od rodzaju środowiska oraz parametrów konfiguracyjnych rzeczywistych urządzeń Podstawowymi parametrami węzłów sprawdzanymi podczas kampanii symulacyjnych były:
- Czułość odbiornika
- Długość jednej rundy algorytmu zliczania, a także powiązana z nią zakładana liczba stacji
Analiza wyników wykazała, iż najlepsze rezultaty uzyskiwane są przy ustawieniu odbiorników na wysoką czułość, jednak taką, aby ryzyko wyzwolenia fałszywego alarmu (kiedy odbiornik błędnie uznaje, że inny węzeł transmituje sygnał radiowy) spowodowane szumem termicznym było niewielkie. Obniżanie czułości wpływa niekorzystnie na jakość zliczania z powodu pomijania niektórych transmisji (kiedy odbiornik błędnie uznaje, iż nie jest przeprowadzana żadna transmisja, mimo iż inny węzeł w sieci jej dokonuje). Tak więc ustawienie czułości odbiornika będzie kompromisem pomiędzy ryzykiem fałszywego alarmu a ryzykiem fałszywego pominięcia. Podczas wstępnego szacowania ilości węzłów w sieci najlepszą strategią jest taka, która gwarantuje, iż zakładana liczba węzłów nie będzie przekroczona. Należy więc określać maksymalną liczbę węzłów, która może się znaleźć w danej sieci. W takim przypadku, nawet, gdy oszacowana maksymalna liczba węzłów będzie kilkukrotnie większa niż faktyczna liczba aktywnych węzłów w sieci błąd oszacowania nie wzrośnie w znaczącym stopniu (wyniki symulacyjne pokazują, że przy zakładanej maksymalnej liczbie węzłów przekraczającej o 500\% rzeczywistą liczbę węzłów, pomyli się maksymalnie o około 30\%). Wzrost ten jest zależny od stopnia zainterferowania środowiska: czym poziom interferencji jest większy, tym szybciej przeszacowanie negatywnie wpłynie na dokładność zliczania. Efekt ten został zobrazowany na poniższym wykresie

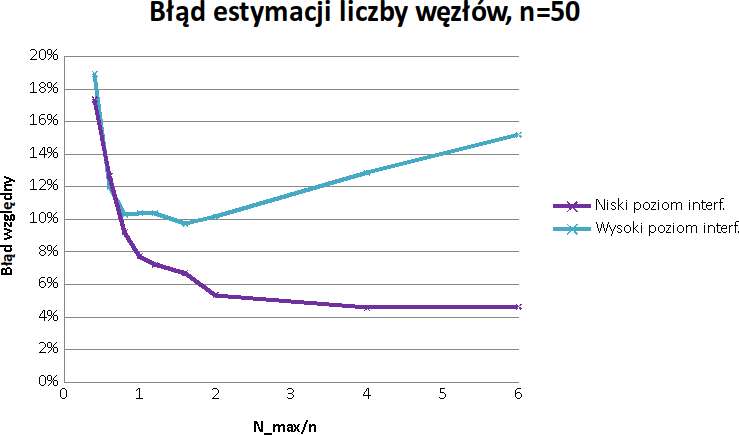
Wykres zależności średniego błędu względnego szacowania liczby węzłów w sieci w zależności od stosunku zakładanej liczby stacji ($N\_max$) do rzeczywistej liczby stacji ($n=50$), dla przypadku niskich i wysokich interferencji
ocena przydatności algorytmu w realnych zastosowaniach Symulacje sieci radiowej pokazują, że algorytm dobrze spełnia stawiane przed nim wymagania, w szczególności:
- Błąd względny zliczania utrzymuje się na akceptowalnym poziomie dla dużego zakresu przeszacowania maksymalnej liczby węzłów oraz dużego poziomu interferencji zewnętrznych
- Algorytm umożliwia działanie węzłów przed ich dokładnym zsynchronizowaniem, co jest bardzo istotną cechą na etapie inicjalizacji sieci
- Algorytm działa w oparciu o wykrywanie fali nośnej, a takie rozwiązania, z racji prostoty i braku konieczności dekodowania informacji, zazwyczaj są bardziej energooszczędne od skomplikowanych algorytmów

Zadania 3 i 4

Inicjalizacja grupy w sieci single-hop

Implementacja