Zadania 11 i 12

Do analizy zadania przystąpiono korzystając z nabierającego ostatnio popularności modelu ,,beeping model''. Jest on wyjątkowo wymagający ze względu na zagłuszanie. Zakłada się, że wiadomości nie są sekwencją bitów modulujących sygnał radiowy, lecz jedynie \underline{pojedynczym} sygnałem. Dodatkowo, nałożenie się dwóch i więcej sygnałów (beepów) jest tożsame z transmisją tylko jednego. W tym modelu podjęto prace polegające na zbudowaniu mechanizmu identyfikacji stacji przez jedną jednostkę główną. Mechanizm, ze względu na przyjęte obostrzenia, powinien działać pewnie nawet w przypadku częstych zagłuszeń wzajemnych stacji. Zastosowany został model probabilistyczny wysyłania beepów przez stacje tzn. każda z nich transmitowała w momentach określonych właściwym dla stacji prawdopodobieństwem. Algorytm 1 przedstawia pseudokod wysyłania i odbioru beepów. Należy tutaj zaznaczyć, że realizacja techniczna części nasłuchującej może zostać wykonana przez ciągłe monitorowanie poziomów sygnału.

    Algorytm 1: BernouliiBroadcast$(id,p)$

      Inicjalizacja:
        rand seed $\gets h(id,key)$
        $U[1 \ldots T] \gets 0$

      W czasie $t\in \{1, 2, \ldots, T \}$
        if $\mathrm{rand}(0,1) \leq p$
          broadcast beep w momencie $t$
          $U[t] = 1$
        else
          $U[t] = \left\{
          \begin{array}{ll}
            0 & \mbox{brak sygnału beep w momencie } t \\
            1 & \mbox{odebrany został sygnał beep w momencie } t
          \end{array}
          \right.$

    Algorytm 2: Identification$(id,p)$
      
      Identyfikacja urządzeń:
        $U$ - tablica wszystkich odebranych beepów
        $S \gets \emptyset$
        for $id \in \mathrm{ID}$
          rand seed $\gets h(id,key)$
          state $\gets true$
          for $t=1$ to $T$
            if $\mathrm{rand}(0,1) \leq p$ and $U[t] \neq 1$
              state $ \gets false$
          if state = $true$
            $S = S \cup \{id\}$

Analiza algorytmu

Obliczmy prawdopodobieństwo fałszywej identyfikacji stacji. Sytuacja taka zdarza się jeśli stacja o identyfikatorze $id$ jest rozpoznana przez algorytm, ale w rzeczywistości w ogóle nie nadawała. Niech $n$ będzie liczbą stacji oraz $k$ będzie liczbą slotów w których wybrana stacja $s$ nadaje.

Lemat 1: Prawdopodobieństwo, że w algorytmie BernouliiBroadcast$(id,p)$ każda $n$ z $n+1$ stacji wybierze takie same $k$ slotów jak wybrana stacja wynosi $(1-(1-p)^n)^k$.

Dowód: Możemy zauważyć, że nadawanie stacji przebiega zgodnie z rozkładem Bernoullego. Zatem, niech $X$ będzie zmienną losową o rozkładzie Bernoullego z parametrem $p$. Wtedy prawdopodobieństwo, że co najmniej jedna stacja nadaje wynosi $P(X\geqslant 1) = 1-(1-p)^n$. Ponieważ identyfikacja stacji polega na sprawdzeniu, czy w każdym z $k$ slotów przebiegła transmisja stąd otrzymujemy $(1-(1-p)^n)^k$.

Jednak w algorytmie liczba slotów w których stacja $s$ nadaje nie jest stała tylko jest zmienną losową o rozkładnie Bernoullego.

Twierdzenie 1 Prawdopodobieństwo fałszywej identyfikacji przez algorytm 1 wynosi \begin{equation} \label{eqn:prfalse} (1-p(1-p)^n)^T. \end{equation}

Dowód: Niech $Y_i$ będzie zmienną losową o rozkładzie Bernoullego $\mathcal{B}(T,p)$ i przedstawia liczbę slotów w której $i$-ta stacja nadaje. Wtedy z lematu~\ref{lem:chpr} otrzymujemy, że prawdopodobieństwo fałszywej identyfikacji wynosi \begin{equation*} \sum_{k=0}^n (1-(1-p)^n)^k P(Y_i=k)~. \end{equation*} Zatem \begin{equation*} \sum_{k=0}^m (1-(1-p)^n)^k \binom{m}{k}p^k(1-p)^{n-k} = (1-p(1-p)^n)^T~. \end{equation*}

Korzystając ze wzoru (\ref{eqn:prfalse}) możemy zminimalizować błąd fałszywej identyfikacji przez znalezienie optymalnego prawdopodobieństwa nadawania $p$. Obliczając pochodną i przyrównując ją do zera, po przekształceniach dochodzimy do równania \begin{equation*} -(1 - p)^n + n (1 - p)^{n-1} p = 0~. \end{equation*} Rozwiązując powyższe równanie otrzymujemy, że \begin{equation*} p_{opt} = \frac{1}{n+1}~. \end{equation*} Podstawiając optymalne prawdopodobieństwo (\ref{eqn:prfalse}), otrzymujemy \begin{equation*} \left(1-\frac{\left(1-\frac{1}{n+1}\right)^n}{n+1}\right)^T \approx \left(1-\frac{1/e}{(n+1)}\right)^T~. \end{equation*} Celem naszym jest minimalizacja fałszywych identyfikacji dlatego rozwiążmy powyższe wyrażenie względem parametru $T$ przyrównując je do $1/n$. Stąd otrzymujemy \begin{equation*} T = \frac{\ln(1/n)}{\ln(1-\frac{1}{e(n+1)})}~. \end{equation*} Zatem, mamy już wyliczone wszystkie parametry potrzebne do działania naszego algorytmu. W dalszej części można zastanawiać się nad różnymi modyfikacjami przedstawionego algorytmu np. wybór wzorców nadawania ustalony strategią deterministyczną.

Implementacja

Algorytmy opracowane w poprzednich zadaniach cechuje różny wpływ zakłóceń (typu burst i o rozkładzie jednostajnym) na ich działanie. Dla algorytmu $\lambda$-ciągłego CSMA z zadań 1-2 zakłócenia takie są destrukcyjne, ponieważ zakłócają odbiór tym stacjom, które nasłuchują nadchodzących wiadomości a dodatkowo przyczyniają się do zmniejszenia stopnia wykorzystania kanału radiowego (z uwagi na możliwą interpretację zakłóceń jako moment nadawania innej stacji). Algorytm zliczania stacji (zadania 3-4) w obecności zakłóceń obarczony jest błędem prowadzącym do przeszacowania liczby aktywnych stacji. Wystąpienie zakłóceń w czasie wykonywania rozgłaszania (algorytm RBO, zadanie 5-6) będzie prowadzić co najwyżej do wydłużenia czasu potrzebnego na synchronizację węzłów ze strumieniem rozgłaszania. Algorytm wyznaczania tras (zadanie 8) nie jest narażony na zakłócenia, ponieważ jest algorytmem wewnętrznym jednego z węzłów. Algorytm użyty w komunikacji w sieci typu Relay (zadanie 10) jest narażony na zakłócenia, ale uodpornienie może być rozwiązane klasycznymi podejściami np. typu HARQ (Hybrid Automatic Repeat Request). Należy przy tym zaznaczyć, że transmisja w sieci relay występuje w sieci, która przeszła fazę organizacji, a więc zastosowanie rozwiązań typu HARQ jest w takiej sieci możliwe. Z powyższego wynika, że algorytmy z zadań 1-2 oraz 3-4 są tymi, które narażone są na negatywny wpływ zakłóceń w największym stopniu. W raporcie [1] opisano schemat działania sieci urządzeń M2M w ramach sieci komórkowej piątej generacji. W raporcie tym wskazano, że omawiane algorytmy mogą być używane w fazie konfiguracji mikrosieci. Pierwszy algorytm wykorzystywany jest do policzenia węzłów mikrosieci, drugi natomiast jest wykorzystywany m.in. do rozpropagowania informacji o fakcie obecności w sieci węzła o konkretnym identyfikatorze. W ramach zadania 11 opracowany został algorytm identyfikacji węzłów, dla którego zakłócenia wynikające z jednoczesnej transmisji kilku węzłów nie są przeszkodą. W przypadku wykorzystania algorytmu $\lambda$-ciągłego CSMA do przesyłania informacji o tożsamości stacji nadającej, zakłócenia o rozkładzie jednostajnym jak i typu burst będą utrudniały poprawne zdekodowanie przesyłanej wiadomości. Z uwagi na brak konieczności dekodowania odebranej transmisji, w algorytmie badanym w bieżącym zadaniu problem ten będzie dużo mniej istotny. Dla algorytmu zliczania stacji, zakłócenia będą prowadzić do przeszacowania ilości stacji nadających, ponieważ szum oraz chwilowe zakłócenia będą interpretowane jako sygnał od innej stacji. Omawiany algorytm nie może całkowicie zastąpić wspomnianych powyżej rozwiązań, może jednak poprawić działanie sieci w trybie rekonfiguracji [1]. W bieżącym zadaniu przeprowadzono analizę działania algorytmu opracowanego w zadaniu 11, symulując jego działanie zarówno w idealnych jak i w realistycznych warunkach radiowych, tj.:

• modelując tłumienie sygnału pomiędzy węzłami radiowymi
• modelując tłumienie sygnału wynikające z przesłonięć na drodze pomiędzy poszczególnymi węzłami
• modelując zaniki szybkie, powstałe w wyniki ruchu węzłów
• modelując interferencje zewnętrzne poprzez wprowadzenie losowych zakłóceń w momentach nadawania bądź ciszy

Symulacje

Symulacje przeprowadzono wykorzystując symulator opracowany w ramach zadania 13. W ramach symulacji badano jaki jest stopień poprawności identyfikacji zbioru nadających węzłów. Poprawność ta charakteryzowana była przez dwie wartości:

• Stopień poprawnej identyfikacji nadających węzłów (TP, True Positives rate)
• Stopień poprawnej identyfikacji węzłów nienadających (TN, True Negatives rate)

Pierwszy z wymienionych wyżej elementów mówi o tym, jak dobrze algorytm jest w stanie rozpoznać, że stacja o danym ID była aktywna, natomiast TN mówi o tym, jak dobrze algorytm jest w stanie rozpoznać, że dana stacja nie nadawała. W symulacjach założono stałą długość jednej transmisji, równą 10ms. Zasymulowano grupę 10 węzłów, z czego 5 było aktywnych. Zmiennymi parametrami algorytmu były:

• czas trwania jednej rundy: T
• prawdopodobieństwo nadawania: p

Symulacje w warunkach idealnych

W pierwszej kolejności wykonano symulacje w idealnych warunkach radiowych, aby zrozumieć zachowanie algorytmu. Wyniki uzyskane w takich warunkach oczywiście pokazują stałą, stuprocentową wartość parametru TP, co oznacza, że bez zakłóceń algorytm jest w stanie wykryć aktywność wszystkich stacji. Ciekawe są za to wyniki TN, które spada wraz ze wzrostem wartości p. Dla stałej wartości p, wraz ze wzrostem wartości T, można obserwować wzrost TN.

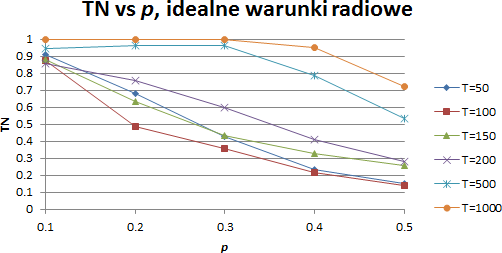
Wyniki symulacji w warunkach idealnych, stopień poprawnej identyfikacji węzłów nienadających (TN)

Symulacje w warunkach realistycznych – brak zakłóceń zewnętrznych

W kolejnym kroku wykonano symulacje w warunkach realistycznych, tj. z uwzględnieniem tłumienia sygnału radiowego, przesłonięć oraz zaników szybkich powstałych w wyniku wzajemnego ruchu węzłów. W symulacjach tych nie modelowano obecności zakłóceń zewnętrznych. W odróżnieniu od przypadku idealnego, nie dla wszystkich przypadków algorytm jest w stanie poprawnie zaklasyfikować wszystkie nadające węzły. Sygnał radiowy momentami jest zbyt słaby, aby po stronie odbiorczej został poprawnie wykryty.

                 

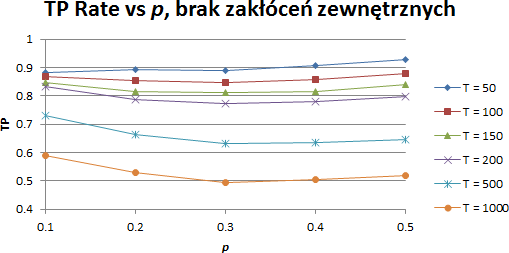
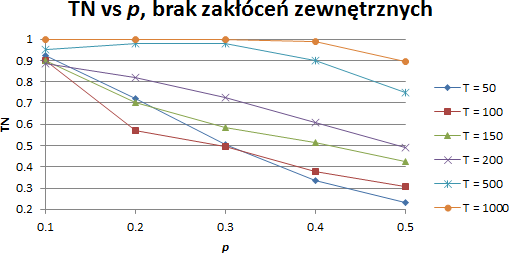
Wyniki symulacji, realistyczne modelowanie kanału radiowego, brak zakłóceń zewnętrznych

Poprawność identyfikacji węzłów aktywnych była większa dla niskich wartości T, natomiast była dość niewrażliwa na zmianę parametru p. Poprawność identyfikacji węzłów nieaktywnych rośnie ze wzrostem T, natomiast spada w miarę wzrostu p.

Symulacje w warunkach realistycznych z obecnością zakłóceń zewnętrznych.

Następnym krokiem było dodanie do symulowanego środowiska interferencji zewnętrznych. Zakłócenia były modelowane jako silne transmisje zewnętrznych sygnałów. Symulacje prowadzono dla różnego stopnia nasycenia środowiska radiowego tymi zewnętrznymi sygnałami. Stopień ten (IR, ang. Interference Rate) określany był jako stosunek czasu trwania interferencji do całkowitego czasu symulacji. Momenty wystąpienia interferencji generowane były zgodnie z rozkładem jednostajnym, miały postać impulsów o czasie równym czasowi nadawania pojedynczej transmisji przez węzły biorące udział w symulacji.

                 

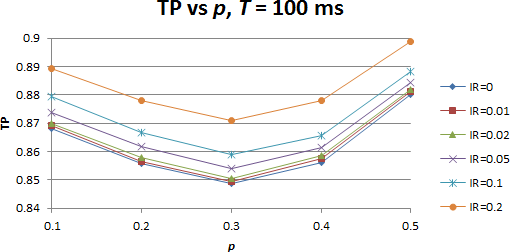
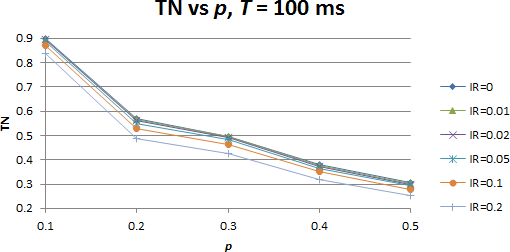
Wyniki symulacji dla różnych wartości parametru IR, dla przypadku T = 100ms

Interferencje nie wpływają w znaczący sposób na poprawność identyfikacji węzłów aktywnych. Stopień poprawności klasyfikacji węzłów jako nieaktywne jest obciążony niewielkim błędem wynikającym z obecności interferencji zewnętrznych, maksymalna zaobserwowana degradacja wynosi 8%.

Symulacje w warunkach realnych, z uwzględnieniem interferencji zewnętrznych –- filtrowanie

W ostatnim kroku zaproponowano wprowadzenie filtrowania wyników jako element uodparniający algorytm na zakłócenia. Założono, że każdy z węzłów będzie wykonywał nadawanie kilkukrotnie, tj. powtórzy kilkukrotnie cały algorytm opracowany w zadaniu 11. Węzeł identyfikujący stacje nadające będzie miał więc do dyspozycji informacje z kilku przebiegów wykonania algorytmu. Zaproponowano więc, aby wyniki z kilku następujących po sobie rund poddać filtrowaniu za pomocą funkcji logicznej OR. Innymi słowy, jeśli węzeł odbiorczy, w ciągu kilku następujących po sobie rundach algorytmu, odebrał w n-tym momencie czasu sygnał, będzie uznawał, że w każdej z rund sygnał został odebrany. Filtrowanie wpływa pozytywnie na identyfikację węzłów, które nadają, natomiast prowadzi też do większej liczby błędnego zaklasyfikowania węzłów nienadających jako aktywnych.

Rules of thumb

Na podstawie symulacji opisanych powyżej, ale także na podstawie symulacji algorytmów opracowanych w poprzednich zadaniach, opracowano wskazówki dotyczące parametryzacji lub modyfikacji algorytmów. Jak wspomniano we wstępie, rozważania ograniczono do algorytmów z zadań 1-2, 3-4, oraz dodatkowo 11-12.\\ Algorytm $\lambda$-ciągły CSMA – dla zastosowań, w których dąży się do zminimalizowania liczby kolizji, dobrym wyborem jest zwiększenie ilości punktów transmisji. W sytuacjach, w których węzły rozsyłają informację nadmiarową (np. gdy kilka czujników informuje o tej samej obserwacji), istotniejsze jest szybkie wysłanie informacji. W takim przypadku lepszym wyborem jest niewielka ilość punktów transmisji. Algorytm zliczania węzłów – Wstępnie założony kres górny może prowadzić do dużego błędu w obliczeniach, szczególnie w obecności zakłóceń. Rozwiązaniem może być wprowadzenie kilkuetapowego zliczania węzłów, polegającego na stopniowej zmianie kresu górnego zakładanej liczby stacji. Jak pokazują symulacje, w sytuacji dużego poziomu zakłóceń, względny błąd estymacji ilości stacji zmniejsza się w miarę zbliżania się do wartości realnej. Algorytm identyfikacji węzłów – W przypadku, gdy dla sieci bardziej istotne jest określenie, które stacje na pewno nadają, niż określenie które stacje pozostają nieaktywne, opisane powyżej filtrowanie jest dobrą metodą uodpornienia na zakłócenia. W przypadku, gdy obydwa parametry są tak samo istotne, można zastosować taki generator liczb pseudolosowych, który zapewni, dla ograniczonego zakresu ziaren generatora, przy zakładanej wartości p, wytworzenie takich sekwencji nadawania, które, gdyby zaprezentować je jako sekwencję bitową, będą miały zwiększoną odległość Hamminga. Pozwoli to na wprowadzenie pewnego rodzaju kodowania protekcyjnego.

Bibliografia

1. ``Mikrosieci urządzeń M2M w sieciach piątej generacji'' – raport projektu ODOKRIM