W2: 04.03.2020: Spójność

1. Klasyczne przykłady grafów (oznaczenia: $[n]=\{1,\ldots,n\}$):
   • graf pusty: $E_n = ([n],\emptyset)$
   • graf pełny: $K_n = ([n],P([n]))$
   • graf liniowy: $L_n = ([n],\{\{i,i+1\}:i=1,\ldots,n-1\})$
   • graf cykliczny: $C_n = ([n],\{\{i,i+1\}:i=1,\ldots,n-1\}\cup\{\{n,1\}\})$
2. Podstawowe konstrukcje: $G_1=(V_1,E_1)$, $G_2=(V_2,E_2)$, $V_1\cap V_2=\emptyset$
   • $G_1+G_2 = (V_1\cup V_2, E_1\cup E_2)$
   • $G_1\star G_2 = (V_1\cup V_2, E_1\cup E_2\cup\{\{x,y\}:x\in V_1\land y\in V_2\})$
   • graf krawędziowy: $L(G) = (E,\{\{A,B\}\in[E]^2: A\cap B \neq \emptyset\})$
3. Przykłady grafów:
   • pełen graf dwudzielny: $K_{n,m} = E_n \star E_m$
   • koło: $W_n = C_n \star E_1$
   • hiperkostka: $Q_n = (\{0,1\}^n, \{\{x,y\}: |\{i:x_i\neq y_i\}|=1\})$
   • graf Petersena
     
4. Def: Graf $G=(V,E)$ jest dwudzielny jeśli istnieje rozbicie $X\cup Y = V$, $X\cap Y = \emptyset$ takie, że $E\subseteq \{\{x,y\}: x\in X \land y\in Y\}$
5. Ustalmy graf $G=(V,E,\phi)$.
   • Trasa w grafie $G$: ciąg $x_0e_1x_1e_2\ldots e_nx_n$ taki, że $\{x_0,\ldots,x_n\}\subseteq V$, $\{e_1,\ldots,e_n\}\subseteq E$ oraz $\phi(e_i) = \{x_{i-1},x_i\}$ dla $i=1,\ldots,n$;
     liczbę $n$ nazywamy długością trasy
   • Scieżka w grafie $G$: trasa bez powtórzonych krawędzi
   • Droga w grafie $G$: ścieżka bez powtórzonych wierzchołków
6. Ustalamy graf $G = (V,E,\phi)$. Na zbiorze wierzchołków $V$ określamy relację $$ x\sim y \equiv \text{istnieje trasa od x do y} $$
   • Fakt: $x\sim y \equiv \text{istnieje droga od x do y}$
   • Fakt: $\sim$ jest relacją równoważności
   • Klasy abstrakcji $\sim$ nazywamy składowymi spójnymi grafu $G$
   • Def. $c(G) = |V/\sim|$
7. Graf $G$ jest spójny jeśli $c(G)=1$
8. Tw. Jeśli graf prosty $(V,E)$ jest spójny, to $|E|\geqslant |V|-1$.
   UWAGA: musicie znać dowód tego twierdzenia.

W3: 11.03.2020: Odległość w grafach

1. Odległości w grafie: d(x,y) = długość nakrótszej drogi od x do y;
   Uwaga: musicie umieć udowodnić, że jest to metryka na grafie spójnym
2. Charakteryzacja grafów dwudzielnych: to są takie grafy w których każdy cykl ma parzystą długość.
   Szkic dowodu: (1) Jeśli graf $G(X,Y)$ jest dwudzielny, $x_0 \in X$ i $x_0x_1x_2\ldots x_k$ jest trasą w $G$, to $x_i \in X$ wtedy i tylko wtedy, gdy $2|i$. A z tego wynika, że każdy cykl ma długość parzystą.
   (2) Załóżmy, że każdy cykl w $(V,E)$ ma długość parzystą. Ustalmy wierzchołek $a$. Niech $X = \{x\in V: 2|d(a,x)\}$ oraz $Y = V\setminus x$. Stosunkowo łatwo pokazujemy, że to jest szukane rozbicie.
3. Grafy Eulera (charakteryzacja przez parzystość stopni wierzchołków);
   obejrzyjcie Graph Theory: Euler Paths and Euler Circuits
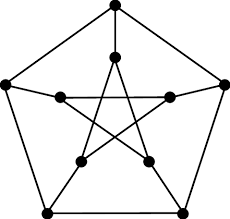
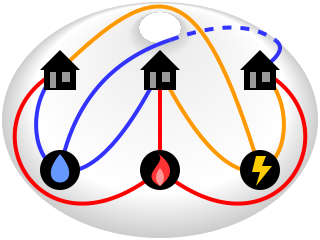
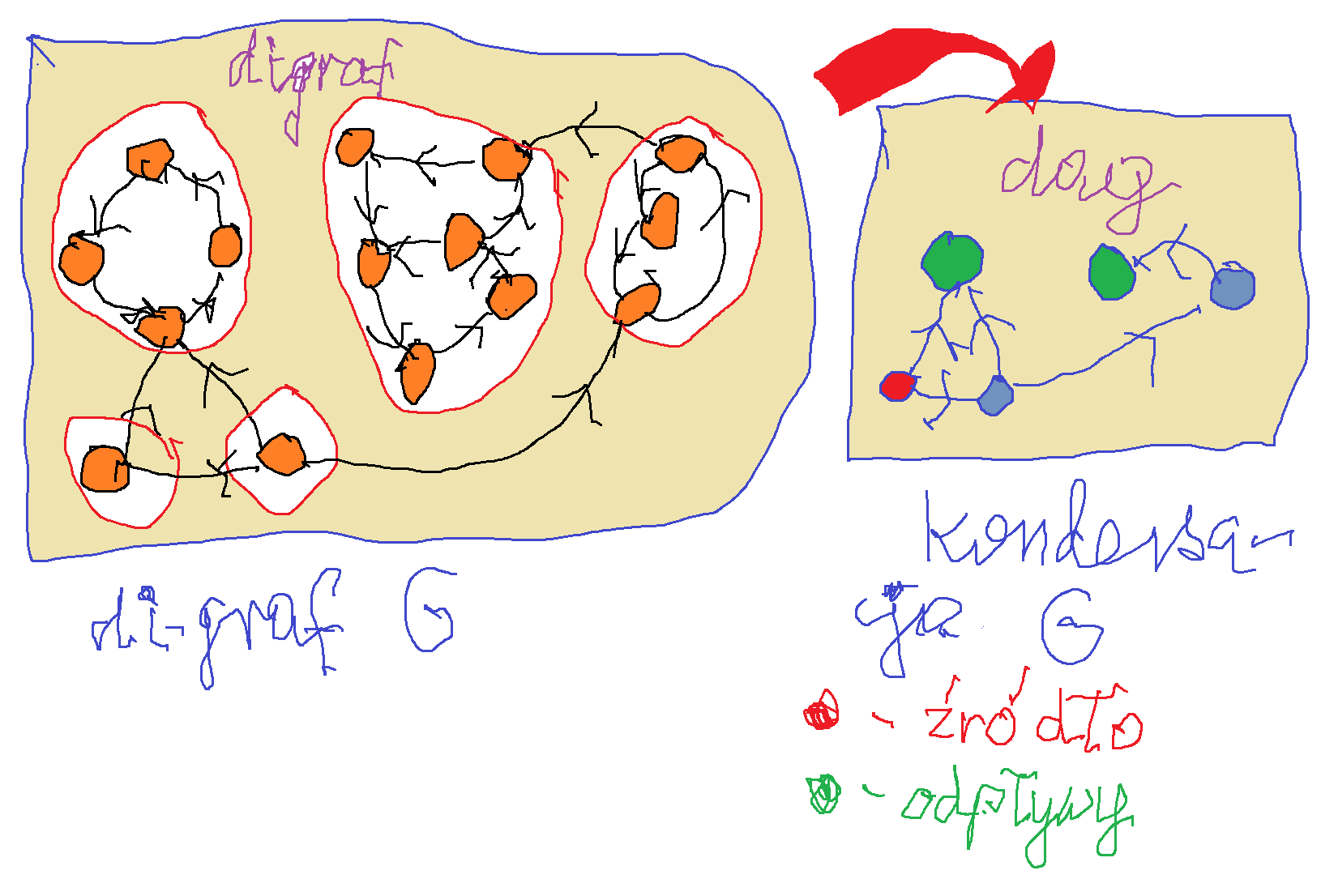
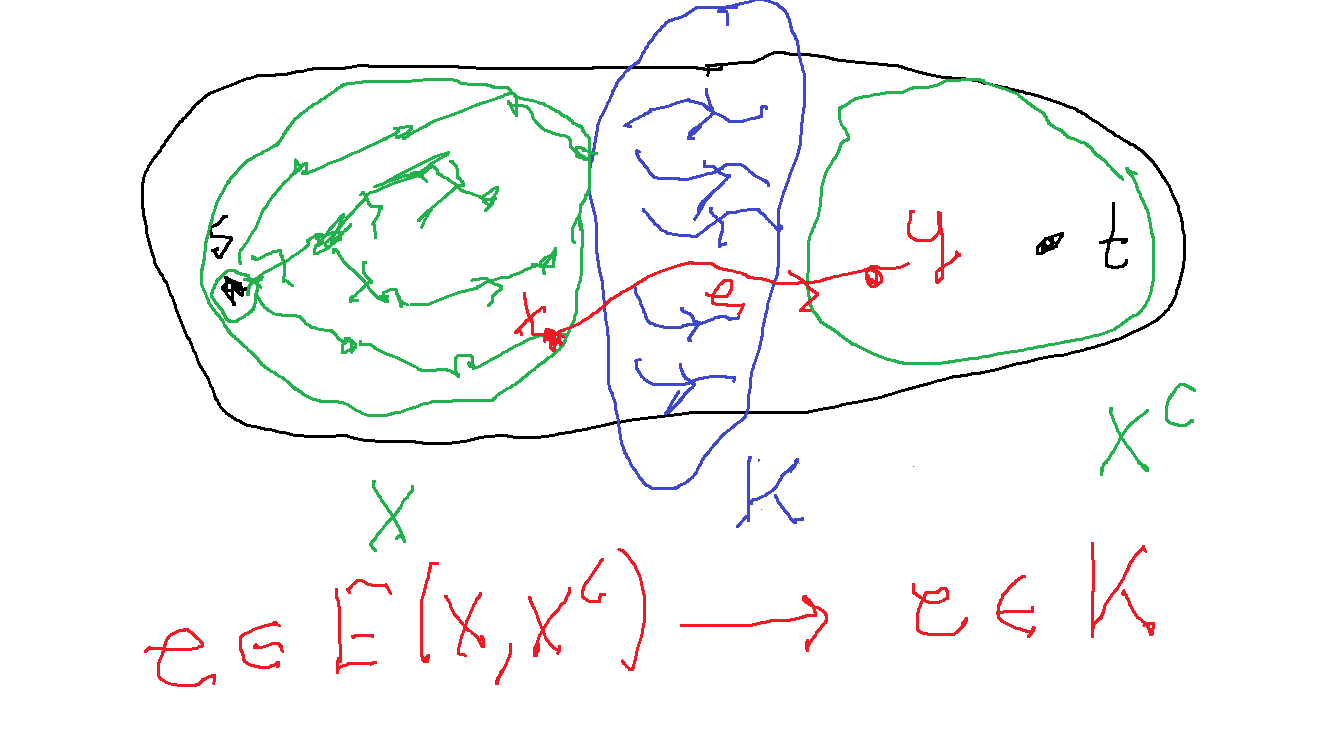
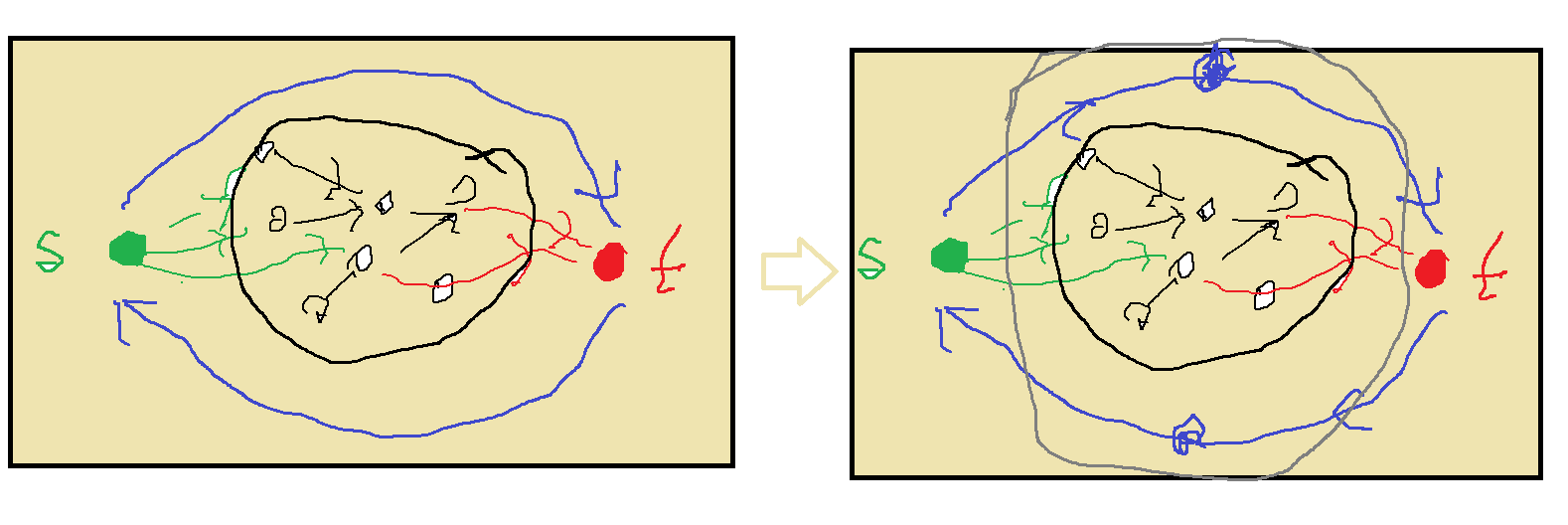
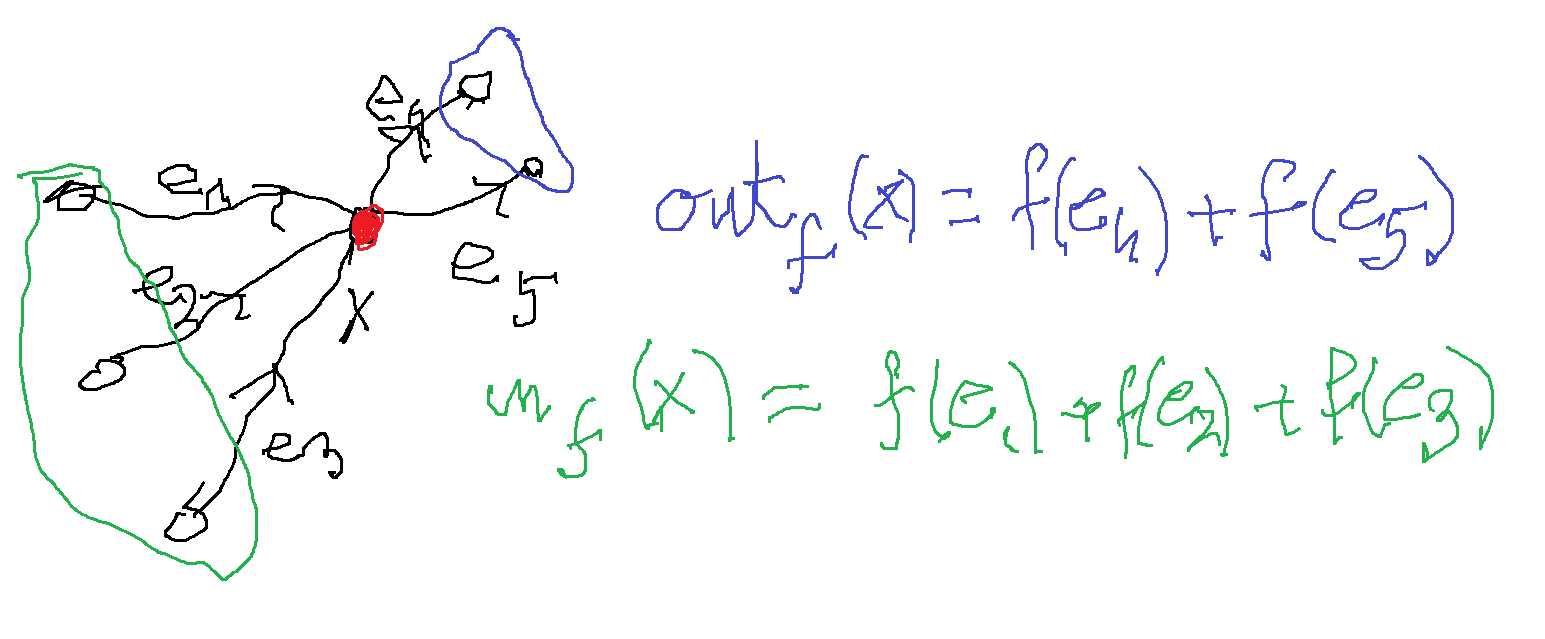4. Grafy hamiltonowskie (twierdzenie Ore i Dirac'a);
   obejrzyjcie Euler and Hamiltonian Paths and Circuits
   
   Twierdzenie Ore: Jeżeli w grafie prostym $G$ o $n \geqslant 3$ wierzchołkach zachodzi nierówność $\deg(v)+\deg(u)\geqslant n$ dla każdej pary niesąsiadujących wierzchołków $u$, $v$, to graf $G$ posiada cykl Hamiltona.
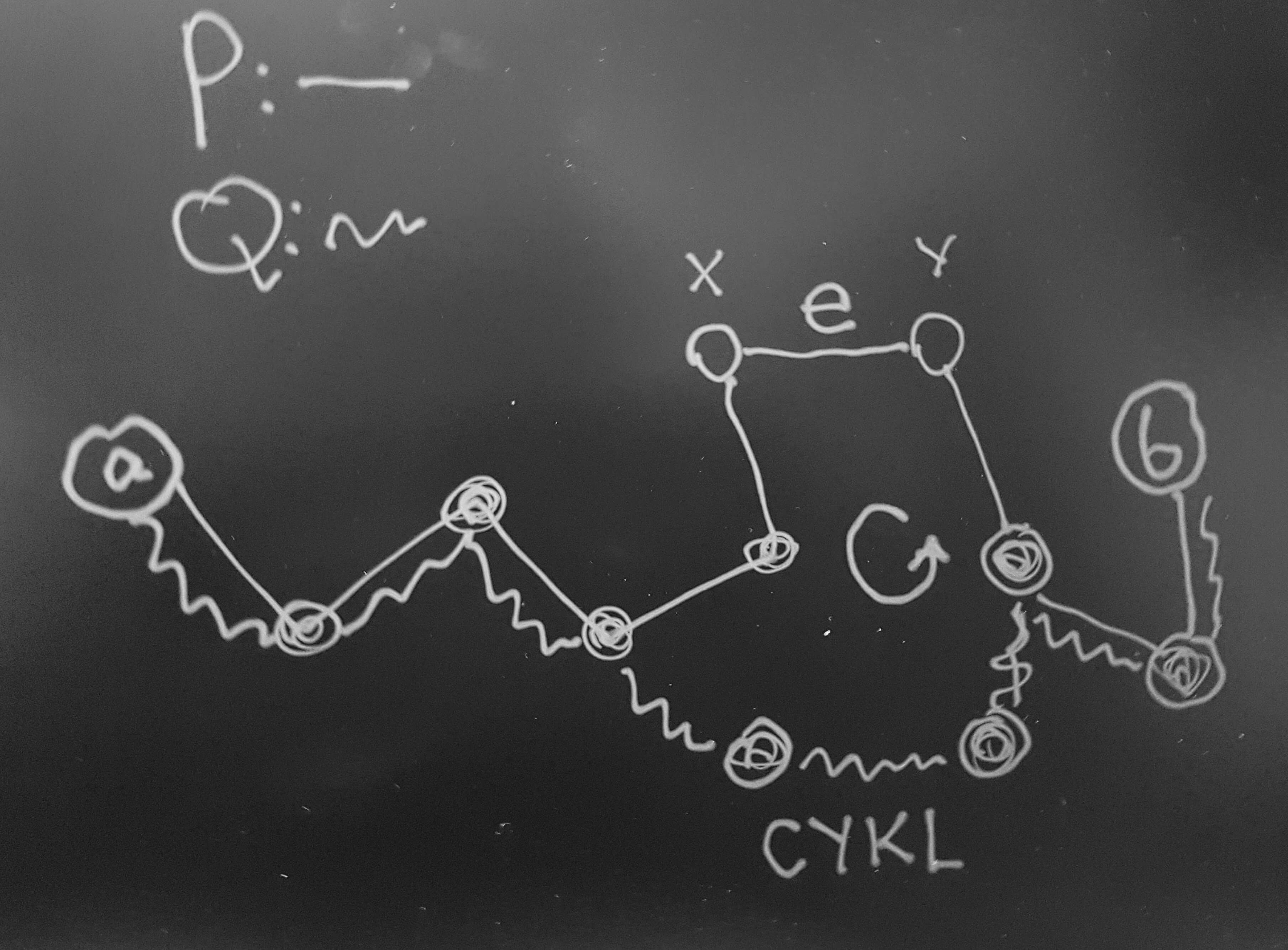
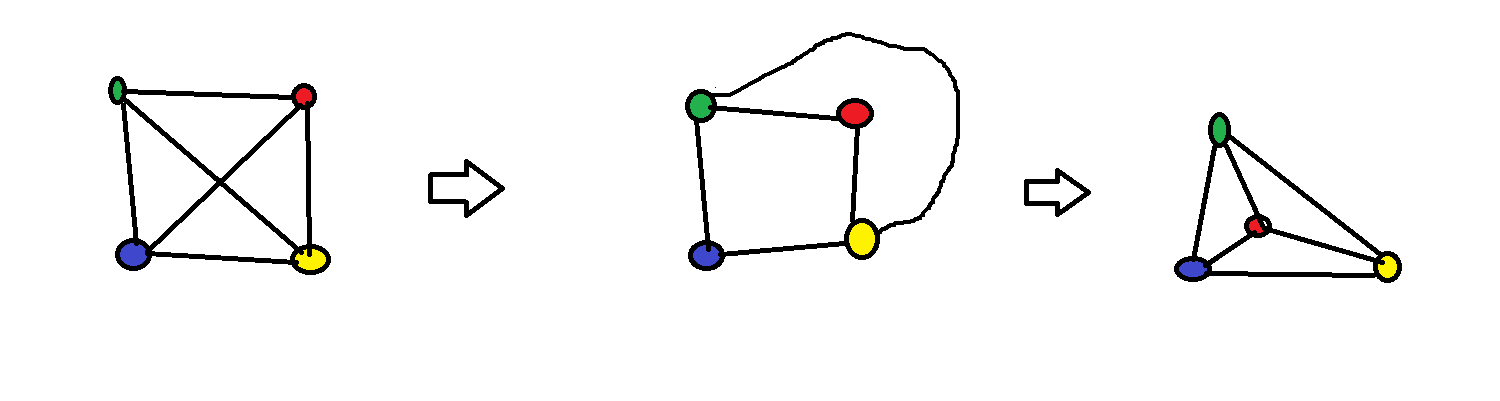
   Szkic dowodu. Załóżmy, że twierdzenie to nie jest prawdziwe dla grafu $G=(V,E)$. Niech $n=|V|$.
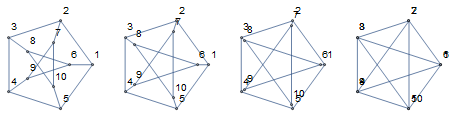
   Krok 1. Zauważmy, że twierdzenie to jest prawdziwe dla grafu pełnego $(V,[V]^2)$. Zatem jeśli do grafu $G$ będziemy dodawali kolejne nowe krawędzie to w pewnym momencie otrzymamy graf z cyklem Hamiltona. Załóżmy, że tymi krawędziami są $e_1,\ldots,e_{k+1}$. Wtedy $G^*=(V,E\cup\{e_1,\ldots, e_{k}\})$ nie jest hamiltonowski, ale $G^{**}=(V,E\cup\{e_1,\ldots, e_{k+1}\})$ ma cykl Hamiltona. Niech $e=e_{k+1} = \{u,v\}$. Co wiemy o grafie $G^*$?. Otóż: (1) nie jest hamiltonowski (2) warunek $\deg(v)+\deg(u)\geqslant n$ jest spełniony (dlaczego ?) (3) mamy drogę $u=x_1, x_2, \ldots, x_n = v$ (bo w $G^{**}$ mamy cykl - wyrzućmy z tego cyklu krawędź $e$).
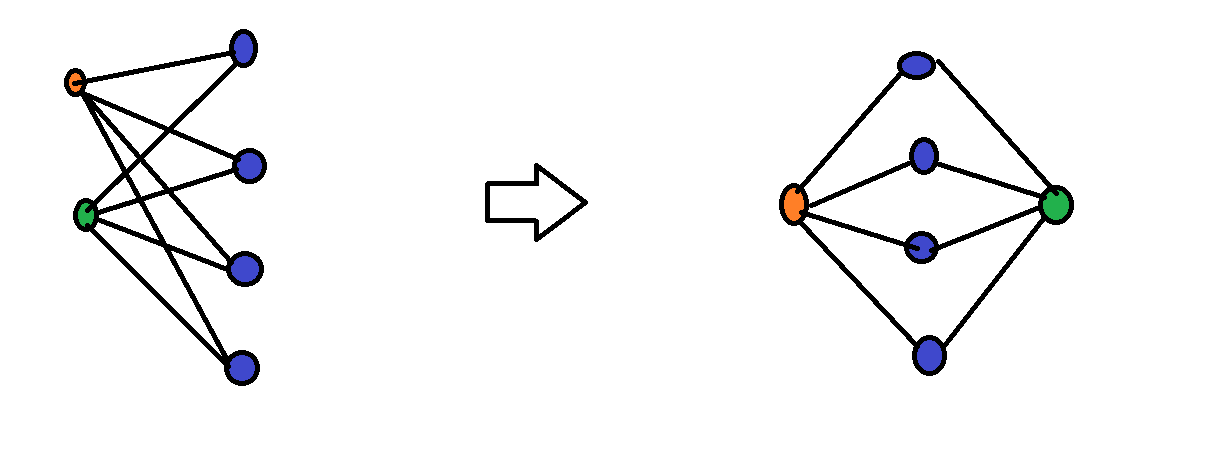
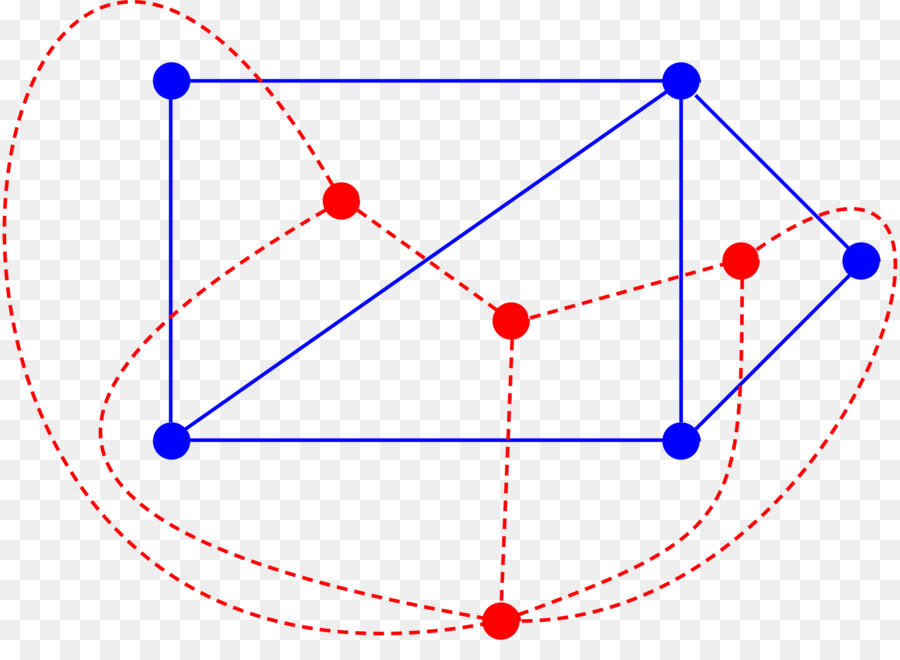
   Krok 2. Przyglądamy się znalezionej drodze $x_1, x_2, \ldots, x_n$ w grafie $G^*$. Niech $A = \{i\in\{1,\ldots,n\}: \{x_1,x_i\} \in E^*\}$, $B = \{i\in\{1,\ldots,n\}: \{x_i,x_n\} \in E^*\}$ ($E^*$ to krawędzie grafu $G^*$). Wtedy $A,B\subseteq \{2,\ldots,n-1\}$ oraz $|A|+|B|\geqslant n$. A teraz proszę spojrzeć na Zadanie 24. Znajdujemy $i\in\{2,\ldots,n-2\}$ takie, że $x_i \in B$ oraz $x_{i+1}\in A$. A z tego już bez trudu konstruujemy cykl długości $n$.

Proponuję abyście samodzielnie zapoznali się z tymi pojęciami i podstawowymi twierdzeniami (książka Wilsona, materiały z YouTube umieszczone wyżej). Dowody twierdzeń możecie sobie odpuścić - rozumowania z książki Wilsona zawierają mocno denerwujące luki.
Poznajcie również algorytm Fleury'ego wyznaczania ścieżki eulerowskiej w grafie (przedtem poznajcie pojęcie mostu w grafie)- pobawcie się tym algorytmem ręcznie na grafach o kilkunastu wierzchołkach (spójrzcie też na YouTube). Dowód poprawności tego algorytmu zrobimy sobie jak się spotkamy w sali wykładowej. Taka wskazówka: na początku bawienia się z algorytmem Fleury'ego postępujcie tak: na jednym rysunku zaznaczajcie kolejnymi liczbami odwiedzane krawiędzie; po każdym kroku algorytmu rysujcie sobie nowy graf z usuniętymi tymi krawędziemi, które już odwiedziliśmy (izolowane punkty ktore mogą się pojawić możecie ale nie musicie usuwać).

Oprócz korzystania z książki Wilsona spójrzcie na stronę Ważniak - tam znajdziecie całkiem fajny przedstawienie tych zagadnień (odpuście sobie, na razie, materiał od twierdzenia Hall'a o skojarzeniach).

Na początku strony umieściłem link do "Questions and Answers". Umówmy się, że pytania związane z tym kursem na które odpowiedzi mogą się przydać innym koleżankom/kolegom będzie zadawać za pomocą tego podsystemu. Możecie w zadawaniu pytań korzystać ze wstawek latex'owych, np. aby wyświetlić $y = 2^x$ wstawcie tekst $\$$y = 2^x$\$$

W4: 18.03.2020: Drzewa

1. Definicja: Graf bez cykli nazywamy acyklicznym. Lasem nazywamy dowolny graf acykliczny. Drzewem nazywamy spójny acykliczny graf. Liściem w drzewie nazywamy wierzchołek o stopniu 1.
2. Wniosek: każdy las jest sumą rozłącznych drzew
3. Na poniższym rysunku: (a) przykład drzewa; (b) przykład lasu; (c) przykład grafu spójnego, który nie jest drzewem
   
4. Lemat A. Każde skończone drzewo z co najmniej dwoma wierzchołkami ma co najmniej dwa liście. Po usunięciu liścia z drzewa z $n$ wierzchołkami otrzymujemy drzewo o $n-1$ wierzchołkach.
   Dowód (szkic). (1) Stosujemy fajny (typowy dla teorii grafów) trik: rozważmy drogę $x_1x_2\ldots x_k$ o największej długości (jest taka droga, bo graf jest skończony) i pokazujemy, że $x_1$ i $x_k$ mają stopień równy 1. (2) łatwe: jeśli $\deg(x)=1$, $a,b\in V\setminus \{x\}$, to droga od $a$ do $b$ nie może przechodzić przez $x$.
5. Def. Krawędź $e$ w grafie spójnym $G=(V,E)$ nazywamy mostem jeśli graf $G-e = (V,E\setminus\{e\})$ nie jest spójny.
   Na poniższym rysynku krawędź będąca mostem ma czerwony kolor.
   
   Zauważ, że po usunięciu mostu z grafu z tego rysunku graf rozpada się na dwie składowe spójne. Tak jest zawsze - jest to jedno z zadań któe pojawi się na liście.
6. Lemat B. Jeśli krawędź należy do cyklu to nie jest mostem
7. Twierdzenie. Niech $G=(V,E)$ będzie prostym grafem o $n\geq 1$ wierzchołkach. Następujące zdania są równoważne:

   1. $G$ jest spójny i nie ma cykli (czyli: $G$ jest drzewem)
   2. $G$ jest spójny i ma $n-1$ krawędzi
   3. $G$ ma $n-1$ krawędzi i nie ma cykli
   Na twierdzenie to można spojrzeć tak: mając trzy własności $\{$spójność, acykliczność, posiadanie $n-1$ wierzchołków$\}$ każda dwójka z nich implikuje trzecią.
   Szkic dowodu: (1)->(2) (indukcja po $n=|V(G)|$) Dla $n=1$ jest OK. Zakładamy, że dla grafów $G$ takich, że $|V(G)|=n$ implikacja ta jest prawdziwa. Bierzemy graf $H$ taki, że $|H|=n+1$. Na mocy Lematu A ma on liście. Niech $a$ będzie takim liściem. Rozważamy graf $H-\{a\}$. ...
   (2)->(3)Założmy, że $G$ jest spójny, ma $n-1$ krawędzi ale ma cykl. Weźmy krawędź $e$ z tego cyklu. Na mocy Lematu B krawędź $e$ nie jest mostem. Zatem graf $G-e$ jest spójny. Ale ma on $n-2$ krawędzi. A to jest sprzeczne z ostatnim twierdzeniem z drugiego wykładu.
   (3)->(1)Załóżmy, że $G$ rozkłada się na składowe spójne $V_1,\ldots,V_k$. Niech $n_1=|V_1|$, ..., $n_k=|V_k|$. Każda ze składowych jst spójna i nia ma cykli. Wiemy już, że (1)->(2). Zatem $V_i$ ma $n_i-1$ krawędzi. Więc graf $G$ ma $(n_1-1)+\ldots+(n_k-1)$ krawędzi. Ale $$ (n_1-1)+\ldots+(n_k-1) = (n_1+\ldots+n_k)-k = n - k$$ więc $k=1$.
   Komentarz: wiemy, że jeśli graf spójny ma $n$ wierzchołków, to musi mieć co najmniej $n-1$ krawędzi; zatem drzewo to graf spójny o minimalnej liczbie krawędzi.
8. Twierdzenie: Niech $G=(V,E)$ będzie prostym grafem o $n\geq 1$ wierzchołkach. Następujące zdania są równoważne:
   1. $G$ jest drzewem
   2. dla dowolnej pary wierzchołków $a,b\in V$ istnieje dokładnie jedna droga od $a$ do $b$
   Dowód (szkic)(1)->(2) Załóżmy, że mamy dwie różna drogi $P$ i $Q$ od $a$ do $b$. Niech krawędź $e$ będzie na drodze $P$ ale nie na $Q$. Niech $e=\{x,y\}$. Zbuduj drogę od $x$ do $y$ w $G\setminus\{e\}$; po dodaniu $e$ do tej drogi otrzymamy cykl:
   
   
   (2)->(1) łatwe.
9. Definicja: Graf $T=(V,E_T)$ jest drzewem rozpinającym grafu $G=(V,E)$ jeśli $T$ jest drzewem i $E_T \subseteq E$.
   Na poniższym rysunku jest graf i jedno z jego drzew rozpinających (czarne kreski):
   
10. Twierdzenie. Każdy spójny graf ma drzewo rozpinające.
    Dowód 1 (trochę abstracyjny) Niech $(V,E)$ będzie grafem spójnym. Niech $\mathcal{E}$ będzie rodziną wszystkich podzbiorów $H\subseteq E$ takich, że $(V,H)$ jest spójny. Niech $T$ będzie $\subseteq$-minimalnym elementem $\mathcal{H}$. Wtedy $(V,T)$ jest drzewem.
    Dowód 2 (bardziej algorytmiczny) Usuwajmy kolejno z $E$ krawędzie z cykli tak długo jak jest jakiś cykl. Na mocy Lematu B nie psujemy spójności. A uzyskamy acykliczność. Otrzymamy więc w ten sposób drzewo.
    Na liście zadań będziecie mieli do przemyślenia jeszcze inny sposób budowania drzewa rozpinającego.

W5: 25.03.2020: Drzewa

1. Fakt: Załóżmy, że $G$ jest lasem o $k$ składowych. Wtedy $|E(G)| = |V(G)| - k$
   Dowód: Niech $X_1,\ldots,X_k$ będą składowymi spójnymi lasu $G$. Wtedy $G[X_i] = (X_i,E\cap [X_i]^2)$ jest drzewem. Zatem $$ |E(G)| = \sum_{i=1}^k |E(G[X_i])| = \sum_{i=1}^k (|V(G[X_i])|-1) =\ldots= |E(G)|-k.$$
2. Twierdzenie (Cayley). Niech $n\geq 2$. Zbiór wszystkich drzew na zbiorze $\{1,\ldots\}$ istnieje $n^{n-2}$ drzew.
   Istnieje wiele dowodów tego twierdzenia. Na wykładzie Sarady Herke:Graph Theory: 40. Cayley's Formula and Prufer Seqences part 1/2 (oraz na następnym) jest dowód tego twierdzenia zrobiony za pomocą kodów Prüfer'a. Szkic tego dowodu możecie również również w księżce Wilsona.
   Sprawdzę w najbliższym czasie, czy na wykładzie z Matematyki Dyskretnej mieliście wykładnicze funkcje tworzące; jeśli tak, to umieszczę tutaj krótki dowód tego twierdzenia za pomocą tych metod.
3. Definicja. Niech $G$ będzie grafem.
   1. $\delta(G) = \min\{\deg{x}: x \in V(G)\}$ (minimalny rząd wierzchołka)
   2. $\bar{d}(G) = \frac{\sum_{x\in V(G)} \deg(x)}{|V(G)|}$ (średni rząd wierzchołka)
   3. $\Delta(G) = \max\{\deg{x}: x \in V(G)\}$ (maksymalny rząd wierzchołka)
   Oczywiście mamy: $$ \delta(G) \leq \bar{d}(G) \leq \Delta(G)$$
4. Niech $G$ będzie prostym grafem spójnym.
   1. Ekscentrycznością wierzchołka $v\in V(G)$ nazywamy liczbę $\mathrm{ecc}(x) = \max\{d(x,y): y\in V(G)\}$.
   2. Promieniem grafu nazywamy liczbę $\min\{\mathrm{ecc}(x) : x \in V(G)\}$
   3. Średnicą grafu nazywamy liczbę $\max\{d(x,y): x,y \in V(G)\}$
5. Algorytm wyznaczania ekscentryczności wierzchołka.
   Zakładamy że dla każdego wierzchołka $x$ mamy metodę wyznaczania listy jego sąsiadów N(x). Poniższy algorytm jest zapisany w pythonowskim pseudo-kodzie:

   INPUT : wierzcholek v
   OUTPUT: ekscentryczność wierzchołka v
   1: L=0
   2: visited = [v]
   3: active  = N(v)
   4: while active != []:
   5:    L += 1
   6:    visited += active
   7:    active = [y for x in active for y in N(x) if y not in visited] 
   8: return L
   

   Twierdzenie. Algorytm ten działa poprawnie.
   Dowód: Pokazujemy indukcyjnie, że po wykonaniu linijki 5 mamy active= $\{x \in V(G): d(v,x)=L\}$ przez cały czas działania pętli.
   Metodę tę nazywamy metodą "przeszukiwania grafu wszerz".
   
   Podczas implementacji tego typu algorytmu trzeba uważać na to aby do grupy active (na filmie są one nazywane zapalonymi) nie dorzucić żadnego wierzchołka już odwiedzonego (visited).
   A poniżej to samo ale na siatce $L_{30}\times L_{30}$:
   
   Ideę powyższego algorytmu można zastosować do wielu innych celów, na przykład, do wyznaczania odległości między wierzchołkami w grafach spójnych, to wyznaczenia drzewa rozpinającego grafu (to będzie na liście zadań).

W6: 01.04.2020: Grafy planarne - I

1. Kilka pojęć pomocniczych
   • Krzywa w $\RR^n$: dowolne ciągłe odwzorowanie $\gamma:[a,b]\to\RR^n$ ($a\lt b$).
     Bez straty ogólności możemy zakładać, że $[a,b]=[0,1]$
   • Krzywa Jordana: taka krzywa $\gamma:[a,b]\to\RR^n$, że $\gamma(a)=\gamma(b)$ oraz że $\gamma$ jest różnowartościowe na $(a,b)$. Wyobrażać ją sobie możemy jaka pętlę bez przecięć.
   • Twierdzenie o krzywej Jordana: Każda krzywa Jordana rozdziela płaszczyznę na dwa rozłączne obszary i jest ich wspólnym brzegiem.
     Nie będziemy dowodzili tego twierdzenia. Wbrew pozorom dowod tego twierdzenia jest dosyć trudny (znacznie się upraszcza jeśli założymy coś na temat regularności krzywej, np. że jest ciągle różniczkowalna).
2. Def: Graf $G=(V,E,\phi)$ jest planarny jeśli jego wierzchołki możemy przedstawić punkty płaszczyzny, a krawędzie jako krzywe na płaszczyżnie łączace wierzchołki, przy czym punktami wspólnymi dwóch różnych krawędzi mogą być tylko ich końcowe wierzchołki.
   Na poniższym rysunku widzimy, że graf $K_4$ jest grafem planarnym, co więcej, jego krawędzie możemy zrealizować za pomocą odcinków:
   A na następnym rysunku widzimy, że $K_{2,4}$ jest też grafem planarnym:
   Uwaga 1. Dosyć łatwo można pokazać, że w pojęciu planarności pojęcie łuku można zastąpić krzywymi łamanymi, czyli takimi, które rozbijają się na skończonę liczbę odcinków. Od tej pory zawsze będzimy stosowali takie reprezentacje grafów planarnych.
   Uwaga 2. Można również pokazać, że dowolne krzywe można zastąpić odcinkami. Widzieliśmy to na dwóch powyższych rysunkach.
3. Twierdzenie: Grafy $K_{3,3}$ oraz $K_5$ nie są planarne.
   Dowód w książce Wilsona jest OK. Spójrzcie również na wykład Sarady Herke pt. Planar Graphs
   Uwaga: Pod koniec dzisiejszego wykładu poznamy inny dowód tego twierdzenia.
4. Ustalmy reprezentację planarną grafu. Niech $G$ będzie zbiorem punktów i krawędzie. Jest to zbiór domknięty. Zbiór $\RR^2\setminus G$ rozkłada się na spójne składowe, zwane ścianami:
   
   Na powyższym rysunku mamy graf o czterech ścianach. Jedna z tych ścian jest nieograniczona - wkrótce zrozumiemy dlaczego ją również zaliczamy do ścian.
   Uwaga. Jeśli graf jest drzewem, to jest grafem planarnym i ma tylko jedną ścianę (nieograniczoną):
   
5. Twierdzenie (Euler) Niech $F$ oznacza liczbę ścian, $E$ liczbę krawędzi oraz $V$ liczbę wierzchołków spójnego grafu planarnego. Wtedy

   $$ F-E+V = 2~.$$
   Dowód. Ustalmy liczbę $V$. Dowód robimy indukcją po liczbie krawędzi. Ze spójności grafu wynika, że $E\geq V-1$.
   Jeśli $E=V-1$, to graf jest drzewem, nie ma więc cyklu, więc ma tylko jedną ścianę. No a wtedy $$F-E+V = 1 - (V-1) + V = 2~.$$ Załóżmy więc, że $E\gt V-1$. Wtedy graf ma cykl. Niech $e$ będzie krawędzią z tego cyklu. Krawędź $e$ leży na brzegu dwóch ścian (jedną z nich może być ściana nieograniczona). Usuńmy $e$ z grafu:
   
   Liczba $E$ zmalała o jeden, liczba $F$ zmalała o jeden a liczba $V$ nie uległa zmianie. Wartość wyrażenia $F+E+V$ nie uległa więc zmianie. Więc jest równa $2$.
   UWAGA: Od tej pory będziemy używali oznaczeń $F,E,V$ na liczbę ścian, krawędzi i wierzchołków w grafie planarnym.
6. Wniosek. Wszystkie planarne realizacje grafu spójnego mają taką samą liczbę ścian.
7. Twierdzenie. Niech $G$ będzie prostym grafem planarnym o co najmniej trzech wierzchołkach. Wtedy

   $$E \leq 3\cdot V - 6~.$$

   Ponadto, jeśli graf nie zawiera trójkątów to $E\leq 2 V-4$
   Dowód. Zauważmy, że każda ściana ograniczona jest co najmniej trzema krawędziami. Zauważmy również, że każda krawędź leży na brzegu co najwyżej dwóch ścian. Zatem $$ 3 \cdot F \leq 2 \cdot E $$
   Zróbmy to dokładniej: ponownie zastosujemy metodę sumowania na dwa sposoby. Niech $F_1,\ldots,F_s$ będą ścianami; niech $f_i$ ($i=1,\ldots,s$) oznacza liczbę krawędzi na ścianie $F_i$; niech $e_1,\ldots,e_m$ będą krawędziami. Wtedy $$ 3\cdot F = 3\cdot s \leq \sum_{i=1}^{s} f_i = \sum_{i=1}^s \sum_{j=1}^m ||e_j \text{ jest incydentna z } f_j|| = $$ $$ \sum_{j=1}^m \sum_{i=1}^s ||e_j \text{ jest incydentna z } f_j|| \leq \sum_{j=1}^m 2 = 2\cdot m = 2\cdot E~. $$
   Przepiszmy równość Eulera: $$ 2 = F - E + V $$ pomnóżmy ją przez 3 i zastosujmy poprzednią nierówność $$ 6 = 3 F - 3 E + 3 V \leq 2 E - 3 E + V = -E + 3 V~.$$ Dla dowodu drugiej części skorzystać trzeba z równości $4 F \leq 2 E$ (pokażcie ją równie dokładnie jak poprzednią nierówność).
8. Uwaga: powyższe twierdzenie ma fajny wniosek: liczba krawędzi w grafie planarnym jest dosyć mała, bo ograniczyć ją można przez $3V$, czyli jest rzędu $O(V)$ - to bardzo przydaje się w geometrii obliczeniowej.
9. Zastosowanie 1. Graf $K_{5}$ nie jest planarny.
   Dowód: Gdyby był planarny to $10 = E \leq 3 V - 6 = 3\cdot 5 - 6 = 9$.
10. Zastosowanie 2. Graf $K_{3,3}$ nie jest planarny.
    Dowód: zadanie.
11. Twierdzenie. Załóżmy, że $G=(V,E)$ jest grafem planarnym. Wtedy istnieje wierzchołek $v$ taki, że $\deg(v)\leq 5$.
    Uwaga: ta własność przyda nam się, gdy będziemy zajmowali się kolorowaniem grafów
    Dowód: Załóżmy, że $(\forall v\in V)(\deg(v)\geq 6)$. Wtedy $$ 6\cdot |V| \leq \sum_{v\in V}\deg(v) = 2\cdot E \leq 2\cdot (3\cdot |V| - 2) = 6\cdot |V|-6~, $$ otrzymaliśmy więc sprzeczność.

W7: 08.04.2020: Grafy planarne - II

1. Rzut stereograficzny: ciągła bijekcja między płaszczyzną a sferą bez jednego punktu.
   Tak wygląda rzut stereograficzny trójkąta z płaszczyzny na sferę.
   
2. Fakt: grafy planarne są tym samym co grafy "bez przecięć" na sferze.
   Uwaga: teraz wyraźniej widać dlaczego do ścian grafu planarnego dołączamy również tę scianę nieograniczoną: ona staje się "normalną" ścianą na sferze.
3. Bryła platońska (wielościan foremny) = wielościan o następujących własnościach: (1) jest wypukły (2) każdy wierzchołek jest tego samego rzędu (3) wszystkie ściany są przystającymi wielokątami foremnymi.
   Przykład: sześcian; czworościan foremny
4. Twierdzenie: Jest pięć brył platońskich
   Dowód: Oznaczania: n = rząd (każdego) wierzchołka; m = liczba krawędzi (każdej) ściany; F = liczba ścian; E = liczba krawędzi; V = liczba wierzchołków.
   Mamy:
   (0) $n\geq 3$, $m\geq 3$
   (1) $n\cdot V = 2 \cdot E$ (wzór Eulera)
   (2) $m \cdot F = 2\cdot E$ (każda krawędź jest na brzegu dwóch ścian)
   (3) $F-E+V = 2$ (wzór Eulera)
   Zatem $$ 2 = \frac{2 E}{m} - F + \frac{2 E}{n} = E\left(\frac{2}{m}-1+\frac{2}{n}\right) $$ Z tego mamy $\frac{2}{m}-1+\frac{2}{n} \gt 0$, zatem $\frac{2}{m}\gt 1-\frac{2}{n} \geq \frac23$, więc $m \lt 6$. Podobnie mamy $n\lt 6$. Zatem $m,n\in\{3,4,5\}$. Ograniczyliśmy więc liczbę możliwości do 9. Dalej będziemy eliminować niemożliwe przypadki.
   PRZYPADEK m=3 (ściany są trójkątami): mamy $2=E(\frac23-1+\frac{2}{n})$, czyli $2= E(\frac{2}{n}-\frac13)$; dla $n=3$ otrzymujemy $E=6$ (to jest czworościan foremny); dla $n=4$ otrzymujemy $E=12$ (to jest ośmiościan foremny); dla $n=5$ otrzymujemy $E=30$ (to jest dwudziestościan formeny)
   PRZYPADEK m=4 (ściany są kwadratami): bez trudu sprawdzamy, że to nam daje sześcian
   PRZYPADEK m=5(ściany są pięciokątami foremnymi); otrzymay dwunastościan foremny.
   
   
   Polskie nazwy: czworościan foremny, sześcian, ośmiościan foremny, dwunastościan foremny, dwudziestościan foremny.
5. Definicja: rozdrobnieniem grafu $G$ nazywamy graf który otrzymuje się z grafu $G$ przez zamianę jego krawędzi drogą o jednej lub więcej krawędzi
6. Fakt: Niech $G'$ będzie rozdrobnieniem grafu $G$. Graf $G$ jest planarny wtedy i tylko wtedy, gdy graf $G'$ jest planarny.
7. Twierdzenie (Kuratowski). Graf nie jest planarny wtedy i tylko wtedy, gdy zawiera rozdrobnienie grafu $K_{3,3}$ lub zawiera rozdrobnienie grafu $K_{5}$.
   Twierdzenie to pokazuje, że $K_{3,3}$ i $K_5$ są kanonicznymi przykładami grafów nieplanarnych. Dowód tego twierdzenia jest dosyć trudny. Być może zrobimy go na ostatnim wykładzie.
8. A tu jest link do moich nieudolnych rysunków ze spotkania na Microsoft Teams: Grafy08042020

W8: 15.04.2020: Grafy planarne III i spójność

1. Kontrakcja krawędzi grafu: niech $(V,E,\phi)$ będzie grafem i $e\in E$; niech $\phi(e)=\{a,b\}$; kontrakcją grafu $G$ względem krawędzi $e$ nazywamy graf $G/e$ ze zbiorem wierzchołków $(V\setminus\{x,y\})\cup \{w\}$ (gdzie $w$ jest jakimś elementem nie należącym do $V$), zbiorem krawędzi $E\setminus\{e\}$ oraz fukcją incydentcji $\phi'$ określoną wzorem $$ \phi'(f) = \begin{cases} \{x,w\}& \phi(f)=\{x,a\} \lor \phi(f)=\{x,b\} \\ \phi(f) & \text{w przeciwnym przypadku} \end{cases} $$ Uwaga: formalna definicja jest nieco zawiła, ale intuicja jest prosta: krawędź $\{a,b\}$ ściągamy do jednego wierzchołka.
2. Fakt: Następujące operacje nie zmieniają planarności grafów: usunięcie wierzchołka, usunięciu krawędzi, kontrakcji krawędzi.
3. Def: Graf $G$ jest minorem grafu $H$ ($G \preceq H$) jeśli $G$ może być otrzymany z grafu $H$ za pomocą skończonej liczby operacji usunięcia wierzchołka, usunięcia krawędzi lub kontracji krawędzi.
4. Twierdzenie (Wagner): Graf nie jest planarny wtedy i tylko $(K_{3,3}\preceq G \lor K_5\preceq G)$
5. Przykład: kontrakcja grafu Petersena
   
6. Eliminacja jednego przecięcia grafu $K_{3,3}$:
   
   A teraz obrazek z WIKI ilustujący czym jest topologiczna transformacja powierzchni:
   
   A oto jak graf $K_{3,3}$ wygląda na torusie:
   
7. Powierzchnie orientowalne o małych "genusach" (z WIKI):
8. Definicja: "Genus" grafu = minimalna liczba rączek, które należy dodać do płaszczyzny (lub sfery) potrzebnych do narysowania grafu na tej powierzchni "bez przecięć".
   Fakt: każdy graf (skończony) ma okreslony genus.
9. Twierdzenie: Jeśli graf ma genus $g$ to $$F-E+V = 2 - 2\cdot g~.$$
10. Fakt: Jeśli graf $(V,E)$ jest spójny, $n=|V|\geq 2$ i nie jest grafem pełnym, to istnieje zbiór $X\subseteq V$ taki, że $|X|=n-2$ i $G\setminus X$ nie jest spójny.
    Dowód: Założmy, że $a,b\in V$, $a\neq b$ oraz $\{a,b\}\notin E$. Kładziemy $X=V\setminus\{a,b\}$ i mamy $G\setminus X = (\{a,b\},\emptyset)$.
11. Def: Spójność wierzchołkowa grafu spójnego $G=(V,E)$: $$ \kappa(G) = \begin{cases} n-1 &: G\sim K_{n}\\ \min\{|X|: X \subseteq V \land G\setminus X \text{ nie jest spójny}\} &: \text{nie jest pełny}\end{cases} $$ Uwaga: Z powyższego faktu wynika, że dla dowolnego spójnego grafu prostego $(V,E)$ mamy $\kappa(G)\leq |V|-1$; co więcej: $\kappa(G) = |V|-1$ wtedy i tylko wtedy, gdy graf jest grafem pełnym, czyli, gdy $E=[V]^2$.
12. Def: Spójność krawędziowa grafu spójnego $G=(V,E)$: $$ \lambda(G) = \min\{|Y|: Y \subseteq E \land G\setminus Y \text{ nie jest spójny}\} $$
13. Twierdzenie. Dla dowolnego grafu spójnego $G = (V,E)$ takiego, że $|V|\geq 2$ mamy $\kappa(G)\leq \lambda(G)$
    Dowód: Niech $E'$ będzie zbiorem krawędzi takim, że $G\setminus E'$ nie jest spójny oraz, że $|E'|=\lambda(G)$. Wtedy $G\setminus E'$ ma dwie składowe spójne (dowolna krawędź z $E'$ uspójnia $G\setminus E'$). Oznaczmy je przez $S$ oraz $\bar{S}$.
    Zauważmy że $(\forall x\in S)(\forall y\in\bar{S})(\{x,y\}\in E \to \{x,y\}\in E')$.
    Jeśli $(\forall x\in S)(\forall y \in \bar{S})(\{x,y\}\in E)$ to $\lambda(G) = |S|\cdot |\bar{S}| = |S|(|V|-|S|) \geq |V|-1$ (dlaczego prawdziwa jest ostatnia nierówność ?). Ale $\kappa(G)\leq |V|-1$, więc w tym przypadku dowodzona nierówność jest prawdziwa.
    Załóżmy więc, że są $a\in S$ i $b\in \bar{S}$ takie, że $\{a,b\}\notin E$. Niech $T_1 = \{y \in \bar{S}: \{a,y\}\in E\}$, $T_2 = \{x\in S\setminus\{a\}: (\exists y\in \bar{S})(\{x,y\}\in E\}$. Niech $T=T_1\cup T_2$.
    
    Zauważmy, że $b\in\bar{S}\setminus T$ oraz $a\in S\setminus T$. Usuwając wierzchołki ze zbioru $T$ usuwamy wszystkie krawędzie ze zbioru $E'$. Zbiór $T$ jest więc zbiorem rozspajającym (wierzchołki $a$ i $b$ leżą w różnych komponentach spójnych $G\setminus T$). Ponadto $|T|\leq |E'|$. Zatem $\kappa(G)\leq |E'| = \lambda(G)$.
14. DEF: Niech $A,B\subseteq V$. $(A,B)$-scieżką nazywamy drogę $x_0,x_1,\ldots,x_{n-1},x_n$ w grafie taką, że $x_0\in A$, $x_n\in B$ oraz $\{x_1,\ldots,x_{n-1}\}\cap (A\cup B) = \emptyset$.
    Uwaga: jeśli $A\cap B \neq \emptyset$ i $c\in A\cap B$, to ciąg $(c)$ jest $(A,B)$-ścieżką długości 0.
15. DEF: Niech $A,B\subseteq V$. $(A,B)$-konektorem nazywamy dowolny zbiór parami rozłącznych $(A,B)-ścieżek.
16. DEF: Niech $A,B\subseteq V$. $(A,B)$-separatorem nazywamy dowolny zbiór wierzchołków $X$, taki, że dla dowolnej $(A,B)$-ścieżki $P$ mamy $P\cap X\neq \emptyset$.

W9: 22.04.2020: Twierdzenie Mengera

1. Graf $K_5$ na torusie
   
2. Fakt. Niech $\mathcal{P}$ będzie $(A,B)$-konektorem oraz niech $X$ będzie $(A,B)$-separatorem. Wtedy $|\mathcal{P}|\leq |X|$
3. Oznaczenia. Dla grafu prostego $G$ definiujemy:
   1. $\lambda_G(A,B)$: największa moc $(A,B)$-konektora
   2. $\kappa_G(A,B)$: najmniejszą mocą $(A,B)$-separatora.
4. Wniosek. Jeśli $G=(V,E)$ jest grafem prostym oraz $A,B\subseteq V$ to $\lambda_G(A,B) \leq \kappa_G(A,B)$.
5. Twierdzenie. Jeśli $G=(V,E)$ jest grafem prostym oraz $A,B\subseteq V$ to $$\lambda_G(A,B) = \kappa_G(A,B)~.$$
   Dowód. Część I: zakładamy, że $A\cap B=\emptyset$.
   Przeprowadzimy go indukcją względem $|E|$. Dla $|E|=0$ twierdzenie jest prawdziwe (zarówno separatory jak i konektory są puste).
   Rozważmy więc graf prosty $(G,E)$ i załóżmy, że dla wszystkich grafów postaci $(V,E')$ takich, że $|E'|\lt |E|$ twierdzenie jest prawdziwe.
   1. Niech $k = \kappa_G(A,B)$. Naszym celem jest pokazanie, że istnieje (A,B)-konektor mocy $k$. Niech $e = \{x,y\} \in E$ i niech $G'=(V,E\setminus\{e\})$.
   2. Jeśli $k = \kappa_{G'}(A,B)$ to w grafie $G'$ mamy (A,B)-konektor, który oczywiście jest (A,B)-konektorem w grafie G. Możemy więc założyć, że $\kappa_{G'}(A,B) \lt k$.
   3. Niech $C$ będzie (A,B)-separatorem w grafie $G'$. Mamy $|C|\lt k$. Niech $C_x = C\cup\{x\}$.
      
   4. CLAIM: $C_x$ jest (A,B)-seperatorem w grafie $G$
      
      Dowód claimu: rozważmy dowolną (A,B)-ścieżkę $\mathcal{P}$ w grafie $G$. Jeśli $\mathcal{P}$ jest (A,B)-ścieżką w grafie $G'$ to $\mathcal{P}\cap C\neq\emptyset$. Jeśli zaś $e$ występuje w $\mathcal{P}$, to $x\in\mathcal{P}$, więc $\mathcal{P}\cap C_x\neq\emptyset$. Zatem w obu przypadkach $\mathcal{P}\cap C_x\neq\emptyset$.
   5. Z poprzedniego claimu wynika, że $|C_x|\geq k$, zatem $|C| = k-1$ i $x\notin C$.
   6. Podobnie pokazujemy, że zbior $C_y = C\cup \{y\}$ jest (A,B)-separatorem w grafie $G$.
   7. Wiemy, że $\kappa_{G'}(A,B) \lt \kappa_{G}(A,B)$. W grafie $G$ istnieć więc musi (A,B)-ścieżka zawierająca krawędź $e$. Na ścieżce tej występują oba wierzchołki $x,y$. Możemy założyć, że pierwszym wystąpieniem któregoś z tych dwóch elementów jest $x$.
      Możemy więc założyć, że w grafie $G'$ jest $(A,\{x\})$-ścieżka oraz, że w grafie $G'$ jest $(\{y\},B)$-ścieżka. W grafie $G'$ nie ma zaś ścieżki od $x$ do $y$, gdyż inaczej $C$ nie byłby zbiorem (A,B)-separującym w $G'$.
   8. CLAIM. Każdy $(A,C_x)$ separatorem w grafie $G'$ jest (A,B)-separatorem w grafie $G$.
      Dowód claimu: Niech $Z$ będzie $(A,C_x)$-separatorem w grafie $G'$. Rozważmy dowolną (A,B)-ścieżkę $\mathcal{P}$ grafie $G$. Niech $\mathcal{P}'$ będzie podścieżką ścieżki $\mathcal{P}$ zaczynającą się od elementu zbioru $A$ i kończącą się na pierwszym elemencie zbioru $C_x$. Niech $t$ będzie ostatnim elementem tej podścieżki. Rozważmy dwa przypadki

      • $t\in C$: wtedy $\mathcal{P}'$ jest $(A,C_x)$-ścieżką w $G'$, więc $\mathcal{P}'\cap Z\neq\emptyset$
      • $t=x$: na ścieżce $\mathcal{P}'$ nie ma elementu $y$, więc nie ma również krawędzi $\{x,y\}$; więc ponownie $\mathcal{P}'$ jest $(A,C_x)$-ścieżką w grafie $G'$, więc ponownie $\mathcal{P}'\cap Z\neq\emptyset$
   9. Wniosek: $\kappa_{G'}(A,C_x)=k$
      Dowód. Zbiór $C_x$ jest $(A,C_x)$-separatorem w $G'$. Minimalna moc $(A,C_x)$-separatora jest więc mniejsza lub równa $|C_x|=k$. Ale nie może być ona ostro mniejsza od $k$, gdyż każdy $(A,C_x)$-separator w $G'$ jest (A,B)-separatorem w $G$.
   10. Istnieje więc $(A,C_x)$-konektor mocy $k$. Podobnie: istnieje $(C_y,B)$-konektor mocy $k$.
       Łączymy je i otrzymujemy $(A,B)$-konektor mocy $k$
   Część II: $A\cap B\neq \emptyset$
   Niech $C = A\cap B$, $A'=A\setminus C$, $B'=B\setminus C$. Stosujemy udowodnione twierdzenie dla rozłącznych zbiorów A i B do grafu $G' = G\setminus C$. W $G'$ znajdujemy $(A',B')$-konektor $\mathcal{P}'$ i $(A',B')$-separator $S$ tej samej mocy. Wtedy $\mathcal{P}'\cup C$ jest $(A,B)$-konektorem w grafie $G$ oraz $Z\cup C$ jest $(A,B)$-separatorem w $G$ i oba te zbiory mają tą samą moc.
   KONIEC DOWODU.
   To co przedstawiłem wyżej jest rozpisaną wersją dowodu Goringa z pracy Short proof of Menger’s Theorem. Przyznać muszę, że zrozumienie wszystkich detali dowodu Goring zajęła mi sporo czasu.
6. Dwie ścieżki $x_0=a,x_1,x_2,\ldots,x_{n-1},x_n=b$ i $y_0=a,y_1,y_2,\ldots,y_{m-1},y_m=b$ nazywamy wewnętrznie rozłączne jeśli $\{x_1,\ldots,x_{n-1}\}\cap\{y_1,\ldots,y_{m-1}\} = \emptyset$.
7. Twierdzenie (Menger - wersja wierzchołkowa). Niech graf $G=(V,E)$ będzie grafem prostym, $x,y\in V$ i $\{x,y\}\notin E$. Wtedy następujące dwie liczby są równe:

   1. maksymalna liczba $xy$-ścieżek parami wewnętrznie rozłącznych
   2. minimalna moc zbioru $X \subseteq V\setminus \{x,y\}$ takiego, że dla każdej $xy$-ściezki $P$ mamy $Z\cap P \neq \emptyset$
   Dowód. Niech $A = \mathcal{N}(x)$ i $B = \mathcal{N}(y)$. Na mocy poprzedniego twierdzenia mamy (A,B)-konektor i (A,B)-separator tej samej mocy. Każdą ścieżkę ze znalezionego (A,B)-konektora możemy poprawić (jeśli trzeba) do ścieżki bez elementów x i y. Znaleziony (A,B)-separator nie może więc zawierać ani x ani y. Aby zakończyć dowód należy do wszyskich ścieżek ze znalezionego (A,B)-konektora dokleić na początku x i na końcu y.
8. Zadanie: dlaczego w powyższym twierdzeniu zakładamy, że $\{x,y\}\notin E$ ?
9. Twierdzenie (Menger - wersja krawędziowa). Niech graf $G=(V,E)$ będzie grafem prostym, $x,y\in V$. Wtedy następujące dwie liczby są równe:

   1. maksymalna liczba $xy$-ścieżek parami krawędziowo rozłącznych
   2. minimalna moc zbioru krawędzi $Y \subseteq E$ takiego, że każda $xy$-ścieżka zawiera jakąś krawędź z $Y$
   Dowód. Stosujemy udowodnione twierdzenie do grafu $L(G)$ oraz zbiorów $A=\{e\in E: x\in e\}$ oraz $B=\{e\in E: y\in e\}$.

W10: 29.04.2020: Twierdzenie Mengera: II

1. Twierdzenia Mengera są prawdziwe dla dowolnego grafu !!!
2. Def. Pełnym skojarzeniem (z $C$ do $D$) w grafie dwudzielnym $G=G(D,C)$ nazywamy dowolną różnowartościową funkcję $f:D\to C$ taką, że $\forall x\in D)(\{x,f(x)\} \in E(G)$.
3. Def. Niech $G=G(D,C)$ będzie grafem dwudzielnym. Dla $X\subseteq D$ określamy $$\mathcal{N}(X) = \{y\in C: (\exists x\in X)(\{x,y\}\in E(G)\}$$
4. Prosta obserwacja: jeśli istnieje pełne skojarzenie w grafie dwudzielym $G=G(D,C)$, to dla dowolnego $X\subseteq D$ mamy $|X|\leq |\mathcal{N}(X)|$.
5. Twierdzenie Hall'a (o małżeństwach). Niech $G=G(A,B)$ będzie grafem dwudzielnym. Następujące warunki są równoważne

   1. istnieje pełne skojarzenie w grafie $G$ z $A$ do $B$
   2. $(\forall X\subseteq A)(|X|\leq |\mathcal{N}(X)|)$
   Dowód. Wiemy już, że (1) implikuje (2). Zajmiemy się odwrotną implikacją. Załóżmy więc, że (2) jest prawdziwa. Rozważamy następujący graf $G'$: jego wierzchołkami są zbiory $A\cup B\cup\{a,b\}$ ($a$ i $b$ są jakimiś elementami nie należącymi na $A \cup B$); jego krawędziami jest zbiór $$ E(G) \cup \{\{a,x\}:x \in A\} \cup \{\{y,b\}:y \in B\}~. $$ (narysuj sobie ten graf lub spójrz do notatek z wykładu umieszczonych na początku dzisiejszego wykładu) CLAIM: każdy $(a,b)$-separator w grafie $G'$ ma moc $\geq |A|$
   Niech $X$ będzie (a,b)-separatorem. Wtedy $$ |A| = |A\cap X|+|A\setminus X| \leq |A\cap X|+|\mathcal{N}(A\setminus X)| \leq |A\cap X| + |B\cap X| = |X|~. $$
   Zbiór $A$ jest (a,b)-separatorem. Zatem najmniejsza moc separatora to $|A|$. Na mocy twierdzenia Mengera istnieje zbiór wewnętrznie rozłącznych (a,b)-ścieżek mocy $|A|$. Z tego zbioru otrzymujemy pełne skojarzenie.
6. Def. Skojarzeniem w grafie $G$ nazywamy dowolny zbiór krawędzi $\mathcal{E} \subseteq E(G)$ taki, że $(\forall e,f \in \mathcal{E})(e\neq f \to e \cap f = \emptyset)$.
7. Def. $\nu(G) = \max\{|\mathcal{E}|: \mathcal{E} \text{ jest skojarzeniem w } G\}$
8. Def. Pokryciem wierzchołkowym grafu $G$ nazywamy dowolny zbiór wierzchołków $A \subseteq V(G)$ taki $(\forall e \in E(G))(e \cap A \neq \emptyset)$.
9. Def. $\tau(G) = \min\{|A|: A \text{ jest pokryciem wierzchołkowym } G\}$
10. Fakt. $\nu(G)\leq \tau(G) \leq 2 \nu(G)$
    Dowód. Niech $\mathcal{E}$ będzie dowolnym skojarzeniem zaś $A$ dowolnym pokryciem. Wtedy dla każdej krawędzi $e\in\mathcal{E}$ istnieje $a_e\in A \cap e$. Z rozłączności krawędzi ze skojarzenia wynika, że odwzorowanie $e \to a_e$ jest rożnowartościowe. Zatem $|\mathcal{E}|\leq|A|$. To dowodzi pierwszej nierówności.
    Rozważmy teraz skojarzenie $\mathcal{E}$ o największej mocy. Niech $A = \bigcup \mathcal{E}$. Wtedy $|A| = 2 \nu(G)$. Ponadto $A$ jest pokryciem, bo dla dowolnej krawędzi $e$ mamy $e\cap A\neq \emptyset$ (to wynika z maksymalności $\mathcal{E}$). A to pokazuje drugą nierówność.
11. Twierdzenie Koniga (o grafie dwudzielnym). Jeśli $G$ jest grafem dwudzielnym, to $\nu(G)=\tau(G)$.
    Dowód. Niech $G=G(X,Y)$. Zastosujemy twierdzenie Mengera do zbiorów $A=X$ i $B=Y$.
    Każde skojarzenie w $G$ definiuje rodzinę parami rozłącznych (A,B)-ścieżek. I odwrotnie: każda rodzina parami rozłącznych (A,B)-ścieżek generuje skojarzenie.
    Bierzemy zbiór $\mathcal{P}$ wierzchołkowo rozłącznych (A,B) ścieżek największej mocy, którą oznaczamy przez $k$. Z twierdzenia Mengera wynika istnienie (A,B)-separatora mocy $k$. Każdy separator przecina każdą krawędź. Istnieje więc pokrycie wierzchołkowe mocy $k$.
12. Def: Niech $\mathcal{X}=(X,\preceq)$ będzie częściowym porządkiem,
    1. Podzbiór $L\subseteq X$ nazywamy łańcuchem w $\mathcal{X}$ jeśli $(\forall x,y\in L)(x\preceq y \lor x=y \lor y\preceq x)$
    2. Podzbiór $A\subseteq X$ nazywamy antyłańcuchem w $\mathcal{X}$ jeśli $(\forall x,y\in A)(x\neq y \to (\neg( x\preceq y) \land \neg(y \preceq x)))$
13. Fakt: Jeśli $L$ jest łańcuchem oraz $A$ jest antyłańcuchem, to $|A\cap L| \leq 1$
14. Wniosek. Jeśli $\mathcal{L}$ jest rozbiciem X na łańcuchy i $A$ jest antyłańcuchem, to $|A|\leq |\mathcal{L}|$
15. Twierdzenie Dilworth'a o dekompozycji. Dla dowolnego skończonego częściowego porządku $\mathcal{X}=(X,\preceq)$ następujące dwie liczby są równe:

    1. $\min\{|\mathcal{L}|:\mathcal{L} \text{ jest rozbiciem X na łańcuchy}\}$
    2. $\max\{|A|: A \text{ jest antyłańcuchem w } \mathcal{X}\}$
    Dowód. Niech $\mathcal{X}=(X,\preceq)$ będzie częściowym porządkiem. Definiujemy graf $G$: $V=\{x^{-}:x\in X\} \cup \{x^{+}:x\in X\}$, $E=\{\{x^{+},y^{+}\}: x \prec y\}$.
    
    To jest graf dwudzielny. Znajdujemy skojarzenie $M$ najwiekszej mocy $k$ (krawędzie zaznaczone na czerwono na drugiej części rysunku, tutaj $k=3$). Powracamy do wyjściowego częściowego porządku (trzecia część rysunku). Otrzymujemy rozbicie $\mathcal{L}$ na zbioru $X$ na łańcuchy. Niech $C$ będzie zbiorem najmniejszych elementów w tych łańcuchach. Wtedy $|X-C| = |M|$ (!!!) oraz, oczywiście, $|C|=|\mathcal{L}|$. Zatem $|\mathcal{L}| = |X|-|M| = |X|-k$.
    Na mocy twierdzenia Koniga mamy pokrycie wierzchołkowe $A$ grafu $G$ mocy $k$. Niech $B = \{x\in X:x^{+}\in A \lor x^{-}\in A\}$. Wtedy $|B| \leq |A|=k$.
    CLAIM : $X\setminus B$ jest antyłańcuchem.
    Załóżmy, że $x,y\in X\setminus B$ i $x\neq y$. Gdyby $x\prec y$, to $\{x^{+},y^{-}\}\in E$, więc $\{x^{+},y^{-}\}\cap A\neq\emptyset$, więc $x\in B$ lub $y\in B$. Podobnie, nie jest możliwe aby $y\prec y$.
    Zbiór $C=X\setminus B$ jest więc antyłańcuchem w $\mathcal{X}$, oraz $$ |C| = |X\setminus B| = |X| - |B| \geq |X| - k~, $$ Zatem: istnieją rozbicie $\mathcal{L}$ na łańcuchy oraz antyłańcuch $C$ takie, że $|C|\geq |\mathcal{L}|$, co kończy dowód.