JCI: Logika

Zagadnienia omówione na wykładzie

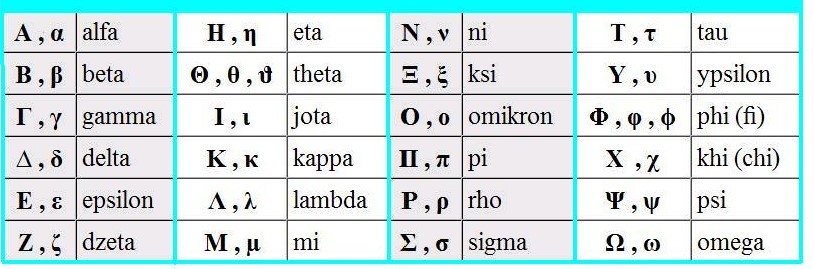
ZADANIE: Naucz się całego alfabetu greckiego.

Podstawowe tautologie
1. ...
2. Prawa de Morgana:
  $$\models(\neg (p\land q) \IFF (\neg p \lor \neg q))$$ $$\models(\neg (p\lor q) \IFF (\neg p \land \neg q))$$
3. Prawo eliminacji implikacji:
  $$\models((p\to q) \IFF (\neg p \lor q)$$
4. ...
Tw. Jeśli $\models\phi(p_1,\ldots,p_n)$ i $\alpha_1,\ldots,\alpha_n$ są dowolnymi zdaniami, to również $\models\phi(p_1/\alpha_1,\ldots,p_n/\alpha_n)$.
Uwaga: na razie zostawiliśmy to bez dowodu.
Def. $\alpha\equiv\beta$ jeśli $\models(\alpha \IFF \beta)$
Fakt: Za pomocą spójników $\land$ i $\neg$ można zdefiniować pozostałe spójniki logiczne
Spójnik Shefera i kreska Pierce'a
Spójnik XOR: $p\oplus q = (p\land\neg q) \lor (\neg p \land q)$

Zastosowanie tautologii $(p \oplus) \oplus q) \equiv p$ do kodowania informacji.
Synteza formuł ($\pm$ "każdą tabelką 0-1 można wyrazić za pomocą formuły")
Uogólnione prawa de Morgana:
1. $\neg(p_1\lor\ldots\lor p_n) \equiv (\neg p_1 \land\ldots\land \neg p_n)$
2. $\neg(p_1\land\ldots\land p_n) \equiv (\neg p_1 \lor\ldots\lor \neg p_n)$
Literały, postać dyzjunkcyjno normalna zdania, postać koniunkcyjno normalna zdania
Problem P = NP

Pojęcie dedukcji: $\{\alpha_1,\ldots,\alpha_n\}\models\beta$
Def. Układ sprzeczny:$\{\alpha_1,\ldots,\alpha_n\}\models (p\land\neg p)$
Reguła wnioskowania Modus Ponens: $\{\alpha,\alpha\to\beta\}\models \beta$.
Reguła rezolucji: $\{\alpha\lor\beta,\neg\alpha\lor\gamma\}\models (\beta\lor\gamma)$
Tw (metoda rezolucji). Następujące zdania są równoważne:
1. $\{\alpha_1,\ldots,\alpha_n\}\models\beta$
2. układ $\{\alpha_1,\ldots,\alpha_n,\neg\beta\}$ jest sprzeczny
Odwrotna notacja polska

Zadanie: Zapisz wyrażania $x*(y*(z*u))$ i $((x*y)*z)*u$ w odwrotnej notacji polskiej

Aksjomat Ekstensjonalności
Fakt: istnieje dokładnie jeden zbiór pusty
Formuły zdaniowe i operacja wyróżniania
Twierdzenie Russela: nie istnieje zbiór wszystkich zbiorów
Podstawowe operacje mnogościowe: $\cup$, $\cap$, $\setminus$
Sprowadzenie równości z rachunku zbiorów do tautologii rachunku zdań
Definicja inkluzji
Tw. Następujące zdania są równoważne:
1. $A \subseteq B$
2. $A \cup B = B$
3. $A \cap B = B$

Zadanie: Sprawdź samodzielnie poprawność definicji działania $\cap$ i $\setminus$.

Dopełnienie do ustalonego zbioru $\Omega$ ($A^c =\Omega\setminus A$ dla $A\subseteq \Omega$)
Prawa de Morgana: $(A\cup B)^c = A^c \cap B^c$, $(A\cap B)^c = A^c \cup B^c$
Składowe rodziny zbiorów $A$ i $B$: $A\cap B$, $A^c\cap B$, $A\cap B^c$, $A^c\cap B^c$
Operacja pary nieuporządkowanej: $\{x,y\}$
Def. Singleton x: $\{x\}:= \{x,x\}$
Fakt. Zbiory z listy $\emptyset, \{\emptyset\}, \{\{\emptyset\}\}, \{\{\{\emptyset\}\}\}, \ldots$ są parami różne.
Operacja zbioru potęgowego $P(X)$: ($A \in P(X)) \equiv (A\subseteq X)$
Rożnica symetryczna zbiorów: $A\triangle B = (A\setminus B)\cup (B\setminus A)$
Tw. Dla każdego zbioru $\Omega$ struktura algebraiczna $(P(\Omega),\triangle)$ jest grupą abelową.
Def.(Kuratowski) $(x,y) := \{\{x\},\{x,y\}\}$
Tw. $((x,y)=(a,b)) \equiv ((x=a)\land (y=b))$

Zadanie: Sprawdź, że struktura $(P(\Omega),\triangle, \cap)$ jest pierścieniem przemiennym z jednością.

Trójki uporządkowane i.t.p.: $(x,y,z) = ((x,y),z)$
Def: $A\times B = \{(a,b): a\in A \land b \in B\}$
Tw. $A\times (B\cup C) = (A\times B) \cup (A\times C)$
Def. Jeśli $\phi$ jest funkcją zdaniową na $X$, to $D_\phi = \{x\in X: \phi(x)\}$
Fakt: $D_{\phi\land\psi} = D_\phi \cap D_\psi$, ...
Def. Jeśli $\phi$ jest funkcją zdaniową na zbiorze $X\neq \emptyset$, to
1. $(\forall x)\phi(x) \equiv^{def} (D_\phi = X)$
2. $(\exists x)\phi(x) \equiv^{def} (D_\phi \neq \emptyset)$
Prawa de Morgana dla rachunku kwantyfikatorów:
1. $\neg (\forall x)\phi(x) \IFF (\exists x)(\neg \phi(x))$
2. $\neg (\exists x)\phi(x) \IFF (\forall x)(\neg \phi(x)$
Twierdzenie
1. $(\forall x)(\phi(x)\land\psi(x)) \IFF ((\forall x)\phi(x) \land (\forall x)\psi(x))$
2. $((\forall x)\phi(x) \lor (\forall x)\psi(x)) \to (\forall x)(\phi(x)\lor\psi(x))$
3. $(\exists x)(\phi(x)\lor\psi(x)) \IFF ((\exists x)\phi(x) \lor (\exists x)\psi(x))$
4. $(\exists x)(\phi(x)\land\psi(x)) \to ((\exists x)\phi(x) \land (\exists x)\psi(x)))$
Uwaga: implikacje odwrotne w (2) i (4) nie są prawdziwe.
Przykład: $X=\NN$, $\phi(x) = "2|x"$, $\psi(x) = "\neg(2|x)"$.

Def. $(\exists a\in A)\phi(x) \equiv (\exists x)(x\in A \land \phi(x))$
Def. $(\forall a\in A)\phi(x) \equiv (\forall x)(x\in A \to \phi(x))$
Tw. $\neg (\exists a\in A)\phi(x) \equiv (\forall x \in A)(\neg \phi(x))$
Tw. $\neg (\forall a\in A)\phi(x) \equiv (\exists x \in A)(\neg \phi(x))$
Diagram funkcji zdaniowej $\phi:\Omega\times\Omega\to\{0,1\}$: $D_\phi=\{(x,y)\in\Omega:\phi(x,x)\}$
Def. Dla $\phi:\Omega\times\Omega \to \{0,1\}$ definiujemy
1. $(\forall x)(\forall y)\phi(x,y) \equiv (\forall x)\left((\forall y)\phi_x(y)\right)$
2. $(\exists x)(\exists y)\phi(x,y) \equiv (\exists x)\left((\exists y)\phi_x(y)\right)$
3. $(\forall x)(\exists y)\phi(x,y) \equiv (\forall x)\left((\exists y)\phi_x(y)\right)$
4. $(\exists x)(\forall y)\phi(x,y) \equiv (\exists x)\left((\exists y)\phi_x(y)\right)$
gdzie $\phi_x(y) = \phi(x,y)$.

Dla dowolnej formuły $\phi = \phi(x,y)$ zachodzą następujące zależności: