Literatura
- Podstawowa
- Ross Kenneth A., Wright Charles R. B., Matematyka dyskretna, Wydawnictwo Naukowe PWN,
- Ronald L. Graham, Donald E. Knuth, Oren Patashnik, Matematyka konkretna, PWN,
- Robin J. Wilson, Wprowadzenie do teorii grafów, PWN,
- Pomocnicza:
- P. Flajolet, R. Sedgewick, Analytic Combinatorics, Cambridge University Press,
- Lista zadań: MDZadania2022.pdf (30.05.2022).
Uwaga: Ta lista będzie się rozszerzać będę tutaj podawał datę ostatniej aktualizacji.
Zasady zaliczania kursu
Ćwiczenia
Zasady zaliczenia ćwiczeń ogłaszają osoby z którymi macie ćwiczenia.
Zadania programistyczne
W trakcie kursu podam kilka zadań programistycznych. Ich realizacja będzie konieczna dla otrzymania oceny 5.5.Egzamin
- Termin I : 27.06.2022 godz. 13:15 - 15:00 s.205 C-1 na platformie Teams.
- Termin II: 07.07.2022 godz. 13:15 - 15:00 s.205 C-1 na platformie Teams.
Do egzaminu będą mogli przystąpić wszyscy studenci, również ci, którzy otrzymali ocenę 2.0 z ćwiczeń. Ocena za kurs będzie wystawiana za pomocą następującego wzoru: $$ K = \begin{cases} 2.0 &: \text{ jeśli } E = 2.0\\ \frac12 (E+\min\{C,5\}) &: \text{ jeśli } E>2.0 \end{cases} $$ gdzie $C$ oznacza ocenę z ćwiczeń zaś $E$ ocenę z egzaminu.
- Osoby które otrzymają ocenę $\geq 4.5$ z ćwiczeń mogą nie przystąpić do egzaminu, ale otrzymają ocenę końcową o $0.5$ stopnia niższą.
- Jeśli ktoś otrzyma ocenę 5.0, a będzie chciał otrzymać 5.5, to będzie musiał odbyć ze mną rozmowę na platformie Teams, na której omówimy wykonane zadania programistyczne.
- Termin I : MD_2020_21_EG1.pdf
- Termin II : MD_2020_21_EG2.pdf
Zagadnienia omówione na wykładzie
04.03.2022: Wstęp
- Zbiory - przypomnienie
- jeśli $A\cap B = \emptyset$, to $|A\cup B| = |A| + |B|$
- $|A\times B| = |A|\cdot|B|$
- $|B^A| = |B|^{|A|}$
- $|P(A)| = 2^{|A|}$
- Analiza dowodu tego, że $|P(A)| = 2^{|A|}$:
Dla $X\subseteq \{0,1,\ldots,n-1\}$ określamy ciąg $(x_0,x_1,\ldots,x_{n-1})$ wzorem $$ x_i = \begin{cases} 1 &: i\in X \\ 0 &: i\notin X\end{cases} $$ i kładziemy $$ c(X) = (x_{n-1},x_{n-2},\ldots, x_1,x_0)_{(2)} = \sum_{i=0}^{n} x_i 2^i $$ Wtedy $c$ jest bijekcją między $P(\{0,\ldots,n-1\})$ a abiorem liczb $\{0,1,2,\ldots,2^n-1\}$. - Def. inj(k,n) = zbiór injekcji ze zbioru $\{1,\ldots,k\}$ w zbiór $\{1,\ldots,n\}$
- Tw. $|inj(k,n)| = \prod_{i=0}^{k-1}(n-i) = \frac{n!}{(n-k)!}$.
- Def. (dolna potęga) $x^{\underline{k}} = \prod_{i=0}^{k-1}(x-i)$
- Wniosek. $|inj(k,n)| = n^{\underline{k}}$
- Def. $[A]^k = \{X\subseteq A: |A|=k\}$
- Def. $\binom{n}{k} = \frac{n!}{k!(n-k)!}$
- Tw. $[\{1,\ldots,n\}]^k| = \binom{n}{k}$
- Generowanie dwuelementowych podzbiorów zbioru $\{1,\ldots,N\}$:
FOR I=1 TO N DO FOR J=I+1 TO N DO print([i,j]) - Fakt: $|A\cup B| = |A| + |B| - |A\cap B|$
- Fakt: $|A\cup B\cup C| = |A| + |B| +|C| - (|A\cap B| + |A\cap C| + |B \cap C|) + |A\cap B\cap C|$
- Tw (zasada włączania-wyłączania)
$$ |\bigcup_{k=1}^{n} A_k| = \sum_{k=1}^{n} (-1)^{k+1} \sum_{T\in[n]^k} |A_T| $$gdzie $A_T = \bigcap_{k\in T} A_k$.
Dowód: następny wykład.
11.03.2022: Zasada włączania - wyłączania
- Przykład: $\{k\in\{1,\ldots,100\}: 2|k \lor 3|k \lor 5|k\}| = \ldots = 74$
- Sprawdzenie (Python):
len([x for x in range(1,101) if (x % 2 == 0) or (x % 3 == 0) or (x % 5 == 0)])
- Dowód zasady włączania-wyłączania. Zrobiliśmy go indukcją po $n$, zaczynając od $n=2$. Przydatne było zapisanie dowodzonego wzoru w następującej postaci: $$ |\bigcup_{k=1}^{n} A_k| = \sum_{T\in P_+([n])} (-1)^{|T|+1}|A_T| $$
- Nieporządki:
- $\pi\in Sym(n)$ jest nieporządkiem jeśli $(\forall k\in [n])(\pi(k)\neq k)$
- Tw. Niech $D_n$ oznacza zbiór nieporządków na $[n]$. Wtedy
$$\frac{|D_n|}{n!} = \sum_{k=0}^{n} \frac{(-1)^k}{k!}$$
- Wniosek: $\lim_n \frac{|D_n|}{n!} = \frac{1}{e}$
- Wzór Eulera dla funkcji $\phi$
- Funkcja $\phi$ Eulera: $\phi(n) = |\{k\in\{1,\ldots,n\}: \text{NWD}(k,n) = 1 \}|$
- Obserwacja: jeśli $n = p_1^{\alpha_1}\cdots p_{k}^{\alpha_k}$, gdzie $p_1 \lt p_2 \lt\ldots\lt p_k$ są liczbami pierwszymi, to liczba $n$ ma $(1+\alpha_1)\cdots(1+\alpha_k)$ różnych dzielników.
- Tw. Jeśli $n = p_1^{\alpha_1}\cdots p_{k}^{\alpha_k}$, gdzie $p_1 \lt p_2 \lt\ldots\lt p_k$ są liczbami pierwszymi i $\alpha_1,\ldots,\alpha_k \geq 1$ to $$ \phi(n) = n \prod_{i=1}^{k}(1-\frac{1}{p_i}) $$
- Wniosek. Funkcja $\phi$ jest multiplikatywna, czyli jeśli $n,m\in\NN^+$ oraz $\text{NWD}(n,m) = 1$, to $$ \phi(n\cdot m) = \phi(n)\cdot\phi(m) $$
- Notatki z wykładu: MD02.pdf
- Zadanie: Sprawdż, że $\phi(p) = p-1$ oraz $\phi(p^\alpha) = p^{\alpha-1}(p-1)$ (gdzie $p$ jest liczbą pierwszą oraz $\alpha \gt 0$)
- Zadanie: Napisz funkcją obliczającą $\phi(n)$ wykorzystującą jej multiplikatywność
- Zadanie: Sprawdź zachowanie się następującej funkcji: $f(n) = \sum_{d|n}\phi(d)$
18.03.2022: Współczynniki Newtona - część I
- Def. $\binom{n}{k} = |[n]^k|$
- Wniosek: $\sum_{k=0}^{n} \binom{n}{k} = 2^n$
- Co już wiemy: $\binom{n}{k} = \frac{n!}{k!(n-k)!} = \frac{n^{\underline{k}}}{k!}$
- Symetria: Jeśli $0\leq k \leq n$, to $\binom{n}{k} = \binom{n}{n-k}$
- Tożsamość Pascala: $\binom{n+1}{k+1} = \binom{n}{k+1} + \binom{n}{k}$
- Trójkąt Pascala
- Tw. $\sum_{k\leq m}\binom{k}{a} = \binom{m+1}{a+1}$
Dowód algebraiczny: indukcja po m
Dowód kombinatoryczny: Podziel $[n+1]^{a+1}$ względem maksymalnego elementu. - Fakt. Jeśli $0\lt k \leq n$ to $\binom{n}{k} = \frac{n}{k} \binom{n-1}{k-1}$
- Wzór dwumianowy Newtona: Jeśli $x,y \in \CC$ i $n\in\NN$ to
$$(x+y)^n = \sum_{k=0}^{n} x^k y ^{n-k}$$
- Wniosek: $2^n = (1+1)^n = \sum_{k=0}^{n} \binom{n}{k}$
- Oznaczenie: jeśli $\phi$ jest zdaniem, to $\|\phi\| = \begin{cases}1 &: \phi \\0 &: \neg\phi\end{cases}$
- Wniosek: $\sum_{k=0}^{n} \binom{n}{k}(-1)^k = (-1+1)^n = \|n=0\|$
- Zadanie $\sum_{k=0}^{a} \binom{n}{k}(-1)^k = (-1)^a \binom{n-1}{a}$
- Fakt: $\sum_{k} k \binom{n}{k} = n 2^{n-1}$
Dowód algebraiczny: korzystamy ze wzoru $\binom{n}{k} = \frac{n}{k}\binom{n-1}{k-1}$
Dowód ANALITYCZNY: $n(1+x)^{n-1} = ((1+x)^n)' = \sum_{k=1}^n \binom{n}{k} k x^{k-1}$
- Notatki z wykładu: MD03.pdf
- Zadanie: Zauważ, że $\int_{0}^{x} (1+t)^n dt = \sum_{k=0}^{n} \int_{0}^{x} \binom{n}{k} t^n dt$; wyprowadź z tego wzoru odpowiednią tożsamość dla współczynników dwumianowych.
18.03.2022: Współczynniki Newtona - część II
- Fakt: $\sum_k\binom{n}{2k} = 2^{n-1} + \frac12 \|n=0\|$
- Tw. Jeśli $w,v \in K[x]$ są wilomianami nad ciałem $K$ stopnia $n$ oraz istnieje $n+1$ parami różnych elementów $x_1,\ldots,x_{n+1}$ ciała $K$ takich, że $w(x_1) = v(x_1), \ldots,w(x_{n+1}) = v(x_{n+1})$, to $w=v$
- Tożsamości Vandermonda: $\sum_{i=0}^{k} \binom{n}{i}\binom{m}{k-i} = \binom{n+m}{k}$
- Toższamość Cauchy'ego: $\sum_{i=0}^{n}\binom{n}{k}^2 = \binom{2n}{n}$
- Def: Dla dowolnej liczby zespolonej $z$ i liczby naturalnej $k$ określamy
$$\binom{z}{k} = \frac{z^{\underline{k}}}{k!} \left(\text{czyli } =\frac{1}{k!} \prod_{i=0}^{k-1}(z-i) \right)$$Uwaga: $\binom{z}{k}$ jest wielomianem zmiennej zespolonej $z$ rzędu $k$.
- Przykład: $\binom{-1}{k} = (-1)^k$
- Wniosek (uogólniona tożsamość Pascala): $\binom{z}{k} = \binom{z-1}{k} + \binom{z-1}{k-1}$ dla $k>0$
- Tw (górna negacja). $\binom{z}{k} = (-1)^k \binom{k-z-1}{k}$
- Wniosek: $\binom{-2}{k} = (-1)^k (k+1)$
25.03.2022: Współczynniki Newtona - część III
- Przykład obliczeń: $$ \binom{-\frac12}{k} = \frac{1}{k!} \prod_{i=0}^{k-1}(-\frac12- i) = (-1)^k \frac{1}{k!} \prod_{i=0}^{k-1}(i+\frac12) = \ldots = (-1)^k \frac{1}{4^k} \binom{2k}{k} $$
- Fakt: Jeśli $k\geq 1$ to $\binom{z}{k} = \frac{z}{k} \binom{z-1}{k-1}$ dla dowolnego $z \in \CC$
- Zadanie: uprość $\binom{\frac12}{k}$
- Wzór Strilinga $n! \approx \sqrt{2\pi n} \left(\frac{n}{e}\right)^n$
- Wniosek: $\binom{2k}{k} \approx \frac{1}{\sqrt{\pi k}} 4^k$
- Wniosek: $\binom{\frac12}{k} \approx (-1)^k \frac{1}{\sqrt{\pi k}}$
- Uogólniony wzór dwumianowy:
$$(1+x)^{\alpha} = \sum_{n\geq 0} \binom{\alpha}{n} z^n, \quad |x|\lt 1$$
- Przykład: $(1-x)^{-2} = \sum_{n\geq 0} \binom{-2}{n}(-x)^n = \ldots = \sum_{n\geq 0}(n+1)x^n$
- Współczynniki Multimianowe: dla naturalnych $a_1,\ldots a_k$ takiego, że $a_1+\ldots + a_k = n$ definiujemy $$ \binom{n}{a_1\: a_2\: \ldots \: a_k} = \frac{n!}{a_1! a_2! \cdots a_k!} $$
- Fakt: $|\{(A,B)\in [n]^a \times [n]^b: A\cap B = \emptyset\}| = \binom{n}{a\: b\: n-(a+b)}$.
Równoważne sformułowanie tej obserwacji: $$ \{(A,B,C): (\{A,B,C\} \text{ jest partycją } [n]) \land (|A|=a)\land (|B|=b) \land (|C|=c) \}| = \binom{n}{a\: b \: c}~. $$ - Powyższą obserwację możemy uogólnić na partycje o większej liczbie składników.
- Przykład: słowo MISSISIPI ma $\binom{9}{1\: 1\: 3 \: 4} = 2520$ anagramów
- ZAPOMNIAŁEM TUTAJ OPOWIEDZIEĆ O JEDNYM WAŻNYM ZASTOSOWANIU WSPÓŁCZYNNIKÓW DWUMIANOWYCH
Od tego zaczniemy następny wykład - Pojęcie $\{\uparrow,\rightarrow\}$ - ścieżki: taki ciąg punktów $((x_i,y_i))_{i=0,\ldots,L}$ o współrzędnych całkowiwtych, że $(x_{i+1},y_{i+1}) = (x_i+1,y_i)$ lub $(x_{i+1},y_{i+1}) = (x_i,y_i+1)$ dla każdego $i=0,\ldots, L-1$
- Ważna obserwacja: Liczba wszystkich $\{\uparrow,\rightarrow\}$- ścieżek zaczynających się w $(0,0)$ i kończących się w $(n,m)$ jes równa $\binom{n+m}{n}$
- Każda $\{\uparrow,\rightarrow\}$-ścieżka zaczynająca się w $(0,0)$ i kończąca się w $(n,m)$ kiedyś musi dotrzeć do "lini" $\{0,1,\ldots,n\}\times \{m\}$. A z tego otrzymujemy $$ \binom{n+m}{n} = \sum_{a=0}^{n} \binom{a+m-1}{a} = \sum_{a=0}^{n} \binom{a+m-1}{m-1} = \sum_{k\lt m+n}\binom{k}{m-1}~, $$ co jest znaną już nam własnością współpczynników dwumianowych.
8.04.2022: Współczynniki Newtona - część IV
- Wzór multimianowy:
$$(x_1+\ldots+x_k)^n = \sum_{\substack{a_1+\ldots+a_k \\ a_1,\ldots a_k\geq 0}} \binom{n}{a_1 \; \ldots \; a_k} x_1^{a_1}\cdots x_k^{a_k}$$
- Obserwacja: powyższy wzór jest uogólnieniem klasycznego wzoru dwumianowego
- Wniosek: $3^n = (1+1+1)^n = \sum\limits_{a+b+c=n}\binom{n}{a\; b\; c}$
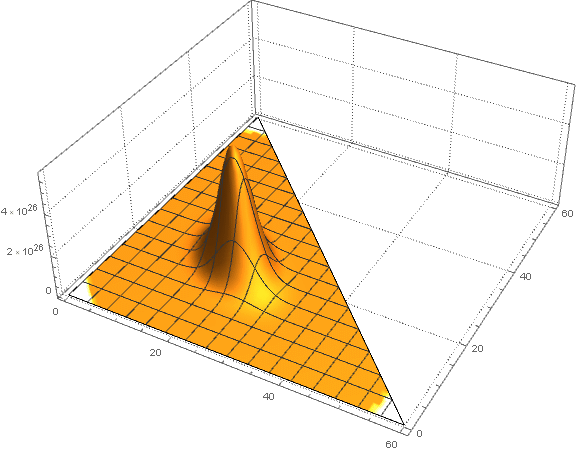
- Wykres wartości współczynników $\binom{60}{a\; b\; 60-(a+b)}$ dla $a\in\{0,\ldots,60\}$ oraz $b \in \{0,\ldots,60-a\}$:
- Przekształcenie $\{\uparrow,\rightarrow\}$ - ścieżek w $\{\nearrow,\searrow\}$ - ścieżki (obrót o kąt $-45^o$)
- Obserwacja: $\{\nearrow,\searrow\}$ - ścieżki można opisać jako ciągi $((k,y_k))_{k=a,\ldots,b}$ takie, że $|y_{k+1}-y_k| = 1$ dla wszystkich $k=a,\ldots,b-1$
- Obserwacja: jeśli $\{\nearrow,\searrow\}$ - ścieżka kończy się w punkcie $(2n,k)$, to $k$ jest liczbą parzystą
- Wniosek: liczba $\{\nearrow,\searrow\}$ - ścieżek od $(0,0)$ do $(2n,2k)$ jest równa $\binom{2n}{n-k}$
- Definicja: Scieżka Dyke'a: $\{\nearrow,\searrow\}$ - ścieżka $((k,y_k))_{k=0,\ldots,2n}$ zaczynająca się w $(0,0)$, kończąca się w punkcie $(2n,0)$ taka, że $(\forall k)(y_k\geq 0)$.
- FAJNY TRICK (odbicie względem linii $y=-1$ od miejsca pierwszego dotarcia do $-1$): liczba złych scieżek (ścieżek, które nie są ścieżkami Dyke'a) od $(0,0)$ do $(2n,0)$ jest równa liczbie ścieżek of $(0,0)$ do $(2n,-1)$. Oto ilustracja tego triku:
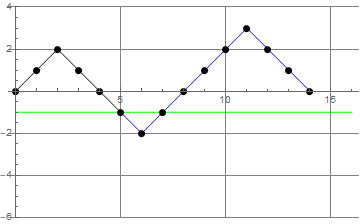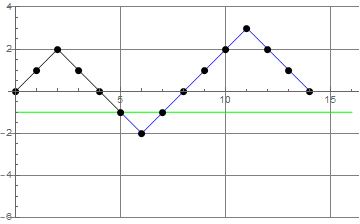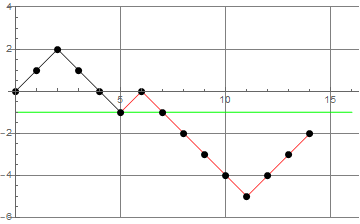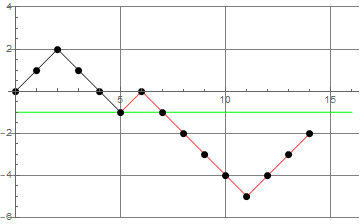
- Wniosek: Liczba $D_n$ ścieżek Dyke'a długości $2n$ jest równa $\binom{2n}{n} - \binom{2n}{n-1}$
- DEF: n-ta liczba Catalana: $C_n = \frac{1}{n+1}\binom{2n}{n}$.
- Twierdzenie: $D_n = C_n$
- Przekłady: $C_0 = 1$, $C_1 = 1$, $C_2 =2$, $C_3 = 5$
- TWIERDZENIE: $$C_{n+1} = \sum_{i=0}^{n} C_i\cdot C_{n-i}$$
- Notatki z wykładu: MD06.pdf
- Artykuł T. Davisa o liczbach Catalana: Catalan Numbers
20.04.2022: Liczby Catalana
- Tw. Liczba różnych wyrażeń któe można zbudować ze zmiennych $x_1,\ldots,x_n$ ($n\geq 1$) oraz jednego działania binarnego $*$ (z zachowaniem kolejności zmiennych) jest równa $C_{n-1}$
- Tw. Liczba drzew binarnych o n liściach: $C_{n-1}$
- Tw. Wypukły $n+2$ - kąt ma $C_n$ trangulacji
- Notacja "duże-O"
$$f=\mathrm{O}(g) \IFF (\exists C)(\exists N)(\forall n \gt N)(|f(n)| \leq C|g(n)|)$$
- Równoważność asymptotyczna
$$f \sim g \IFF \lim_{n\to\infty}\frac{f(n)}{g(n)} = 1$$
- Wzór Stirling
$$ n! \sim \sqrt{2\pi n} \left(\frac{n}{e}\right)^n$$
- Asymptotyka liczb Catalana: $C_n \sim \frac{1}{\sqrt{\pi n}} 4^n$
22.04.2022: Sumy riemanowskie; multizbiory
- Metoda sum riemanowskiech: Jeśli $a,b\in\NN$ i $f:[a,b]\to \RR$ jest niemalejąca (czyli, jeśli $a\leq x \lt y \leq b$, to $f(x)\leq f(y)$) to $$ f(a) + \int_a^b f(x) dx \leq \sum_{k=a}^{b} f(k) \leq \int_a^b f(x) dx + f(b)~. $$
- Przykład: $0+\int_0^n x^2 dx \leq \sum_{k=0}^{n}k^2 \leq +\int_0^n x^2 dx = n^2$, zatem $\frac13 n^3 \leq \sum_{k=0}^{n}k^2 \leq \frac13 n^3 + n^2$, zatem $\sum_{k=0}^{n}k^2 = \frac13 n^3 + O(n^2)$.
- Przykład: $e \left(\frac{n}{e}\right)^n \leq n! \leq e n\left(\frac{n}{e}\right)^n$ (zstosowaliśmy metodę sum riemanowskich do ciągu $a_n = \ln(n!)$
- Def. $n$-ta liczba harmoniczna: $H_n = \sum_{k=1}^n \frac{1}{k}$
- Pokazaliśmy, że $\ln n \leq H_n \leq \ln n + 1$
Dokładniejszy wzór:$$H_n = \ln n + \gamma + \frac{1}{2n} - \frac{1}{12 n^2} + \frac{1}{120 n^4} + O(\frac{1}{n^5}) ~,$$gdzie $\gamma = 0.5772...$ (stała Eulera). - Def. (Multizbiory) $Mult(X) = \{f \in \NN^X: |\{x\in X: f(x)>0\}|\infty\}$.
Rozmiarem multizbioru $f\in Mult(X)$ nazywamy liczbę $|f| = \sum_{x\in X} f(x)$ - Def $\multiset{n}{k} = \binom{n+k-1}{k}$
- Uwaga: $\multiset{n}{k} = (-1)^k \binom{-n}{k}$
- Tw. $|\{f\in Mult(\{1,\ldots,n\}): |f|= k\}| = \multiset{n}{k}$
- Kolejna tożsamość: $\binom{n}{a}\binom{a}{b} = \binom{n}{b}\binom{n-b}{a-b}$
22.04.2022: Prawdopodobieństwo kombinatoryczne. Cykle.
- Def. Kombinatoryczna przestrzeń kombinatoryczna: para $(\Omega,\Pr)$ taka, że $\Omega\neq\emptyset$ zaś $\Pr:P(\Omega)\to[0,1]$ jest funkcją określoną wzorem $$\Pr(A) = \frac{|A|}{|\Omega|}~.$$
- Podstawowe własności
- $0\leq \Pr[A]\leq 1$
- $\Pr[\emptyset]=0,\quad \Pr[\Omega]=1$
- $A\subseteq B \to \Pr[A]\leq\Pr[B]$
- $A\cap B = \emptyset \to \Pr[A\cup B] = \Pr[A] + \Pr[B]$
- Termonologia: zmienna losowa $\equiv$ funkcja z $\Omega$ w $\RR$
- Wartość oczekiwana zmiennej losowej $X:\Omega\to\RR$: $$\EE{X} = \frac{\sum_{\omega\in\Omega} X(\omega)}{|\Omega|}~.$$
- Podstawowe własności
- $X\equiv c \to \EE{X} = c$
- $\EE{a X} = a \EE{X}$
- $\EE{X+Y} = \EE{X}+\EE{Y}$
- Tw. Jeśli $rng(X) = A$, to $\EE{X} = \sum_{a\in A} a \Pr[X=a]$.
- Przykład: $\Omega = \{1,\ldots,6\}^2$, $S((a,b) = a+b$; Wtedy $\EE{S} = 7$
- Tw. Każda permutacja rozkłada się na sumę rozłącznych cykli
- Fakt: jeśli permutacja $\pi\in S_n$ rozkłada się na sumę $k$ cykli, to $\mathrm{sgn}(\pi) = (-1)^{n+k}$.
- Tw. Liczba cykli na zbiorze $\{1,\ldots,n\}$ jes równa $(n-1)!$
- Def. $\StirlingSa{n}{k}$ liczba permutacji ze zbioru $\S_n$ rozkładających się na $k$ cykli.
- Podstawowe fakty
- $\StirlingSa{0}{k} = \|k=0\|$
- $\sum_{k=1}^{n}\StirlingSa{n}{k} = n!$
- $\StirlingSa{n}{1} = (n-1)!$
- $\StirlingSa{n}{n} = 1$
- $\StirlingSa{n}{n-1} = \binom{n}{2}$
- $\StirlingSa{n}{2} = (n-1)! H_{n-1}$
06.05.2022: Liczby specjalne - I.
- Tw. $\StirlingSa{n+1}{k+1} = \StirlingSa{n}{k} + n \StirlingSa{n}{k+1}$
- Def. $x^{\overline{n}} = \prod_{i=0}^{n-1}(x+i)$
- Tw. $x^{\overline{n}} = \sum_{k} \StirlingSa{n}{k} x^k$
- Wniosek. $x^{\underline{n}} = \sum_{k} (-1)^{n+k}\StirlingSa{n}{k} x^k$
- Tw. Na kombinatorycznej przestrzeni probabilistycznej $S_n$ rozważamy zmienną losową $L(\pi) = \text{liczba cykli permutacji } \pi$. Wtedy $$ \EE{L} = H_n~. $$
- Def. (Liczby Stirlinga II rodzaju) $\StirlingSb{n}{k}$ = liczba partycji (rozbić) zbioru $\{1,\ldots,n\}$ na $k$ niepustych składowych.
- Przykład. $\StirlingSb{n}{2} = \frac12(2^n - 2)$
- Tw. $\StirlingSb{n+1}{k+1} = \StirlingSb{n}{k} + (k+1) \StirlingSb{n}{k+1}$
13.05.2022: Liczby specjalne - II.
- Tw. $x^n = \sum_{k} \StirlingSb{n}{k} x^{\underline{k}}$
- Tw. $\StirlingSb{n}{k} = \frac{1}{k!} |Surj(n,k)|$
- Wniosek. $\StirlingSb{n}{k} = \frac{1}{k!}\sum_{i=0}^{k} (-1)^i \binom{n}{k}(k-i)^n$
- Przykład. $\StirlingSb{n}{3} = \frac{1}{6}(3^n - 3 \cdot 2^n +3)$
- Def. Liczby Fibonacciego: $F_0=0$, $F_1=1$, $F_{n+2}=F_{n+1} + F_n$.
- Klasyczne wyprowadzenie wzoru zwartego na $F_n$: wyznaczamy takie $\lambda\neq 0$ takie, że $\lambda^{n+2} = \lambda^{n+1}+\lambda^n$; stwierdzamy, że są dwie takie liczby; oznaczamy je przez $\lambda_1$, $\lambda_2$; dobieramy liczby $A$ i $B$ takie, że $A\lambda_1^n + B\lambda_2^n$ są liczbami Fibonacciego.
- Metoda funkcji tworzących:
- Definiujemy $F(x) = \sum_n F_n x^n$
- Stwierdzamy, że $F(x) = \frac{x}{1-x-x^2}$
- Rozkładamy otrzymany wzór na sumę ułamków prostych: $\frac{x}{1-x-x^2} = A \frac{1}{\omega_1-x} + A \frac{1}{\omega_2-x}$, gdzie $\omega_1 = \frac12(-1-\sqrt{5})$ i $\omega_2 = \frac12(-1+\sqrt{5})$
- Wykonujemy uproszczenia i otrzymujemy WZÓR BINETTA:
$$ F_n = \frac{1}{\sqrt{5}} \left( \left(\frac{1+\sqrt{5}}{2}\right)^n + (-1)^{n+1} \left(\frac{\sqrt{5}-1}{2}\right)^n\right) $$
- Metody wyznaczania liczb Fibonacciego:
Notatki z wykładu: MD11.pdf- Metoda naiwna: rezerwujemy tablicę F[0..n]; kładziemy F[0]=0; F[1]=1; a potem w pętli obliczmy kolejne wartości F[i]=F[-1]+F[i-2].
- Lepsza metoda (pamiętamy tylko "dwie ostatnie wartości": kładziemy X=0, Y = 1; potem w pętli obliczmy [X,Y] = [Y,X+Y] (jednoczesne podstawienie)
- Jeszcze szybsza metoda:
- Zauważamy, że $$ \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} F_{n+1} \\ F_n\end{bmatrix} = \begin{bmatrix} F_{n+2} \\ F_{n+1} \end{bmatrix} $$
- wnioskujemy z tego, że $$ \begin{bmatrix} F_{n+1} \\ F_n \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}^n \circ \begin{bmatrix} 1 \\ 0 \end{bmatrix} $$
20.05.2022: Klasy kombinatoryczne.
- Fakt: $\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}^n = \begin{bmatrix} F_{n+1} & F_n \\F_n & F_{n-1} \end{bmatrix}$ dla $n\geq 1$
Dowód: indukcja - Wniosek (Cassini): $F_{n+1}F_{n-1} - \left(F_n\right)^2 = (-1)^n$.
- Wniosek: $F_{n+m} = F_{n+1} F_m + F_n F_{m-1}$
- Metoda dojścia do wzoru Binett'a za pomocą wartości własnych macierzy $\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}$
- Def. Klasa kombinatoryczna: para $\mathcal{A}=(A,|\cdot|)$ taka że $|\cdot|:A\to\NN$ i
dla każdego $n\in\NN$ mamy $\{a\in A: |a|=n\}|\lt\aleph_0$.
Oznaczenia:- $A_n = \{a\in A: |a|=n\}$
- $a_n = |A_n|$
- $\mathcal{A}(x) = \sum_n a_n x^n$ (funkcja tworząca klasy)
- Przykład: Niech $\mathcal{N} = (\NN, |\cdot|)$, gdzie $|n|=n$. Wtedy $$\mathcal{N}(x) = \frac{1}{1-x}$$
- SUMA KLAS: Zakładamy, że $\mathcal{A}=(A,|\cdot|_A)$ i $\mathcal{B}=(B,|\cdot|_B)$ są klasami kombinatorycznymi oraz $A\cap B = \emptyset$. Określamy $$ \mathcal{A} + \mathcal{B} = (A \cup B, |\cdot|_A \cup |\cdot|_B) $$ Tw. To jest klasa kombinatoryczna oraz $(\mathcal{A} + \mathcal{B})(x) = \mathcal{A}(x) + \mathcal{B}(x)$
- PRODUKT KLAS: Zakładamy, że $\mathcal{A}=(A,|\cdot|_A)$ i $\mathcal{B}=(B,|\cdot|_B)$
są klasami kombinatorycznymi. Określamy
$$
\mathcal{A} \times \mathcal{B} = (A \times B, |\cdot|)
$$
gdzie $|(a,b)| = |a|_A + |b|_B$.
Tw. To jest klasa kombinatoryczna oraz $(\mathcal{A} \times \mathcal{B})(x) = \mathcal{A}(x) \cdot \mathcal{B}(x)$ - Przykład: $\mathcal{N}^2(x) = \frac{1}{(1-x)^2} = \sum_{n\geq 0}(n+1)x^n$
- Przykład: $\mathcal{N}^3(x) = \frac{1}{(1-x)^3} = \sum_{n\geq 0} \binom{-3}{n}(-x)^n = \ldots= \sum_{n\geq 0}\binom{n+2}{2}x^n$
27.05.2022: Klasy kombinatoryczne - II.
- Oznaczenie: $\mathcal{E} = (\{\varepsilon\},|.|)$, gdzie $|\varepsilon| = 0$; mamy $\mathcal{E}(x) = 1$
- Ciągi: $Seq(\mathcal{A}) = \mathcal{E} + \mathcal{A} + \mathcal{A}\times\mathcal{A}+\ldots$
- Fakt. Jeśli $a_0=0$ to $Seq(\mathcal{A})$ jest klasą kombinatoryczną oraz $$ Seq(\mathcal{A})(x) = \frac{1}{1-Seq(\mathcal{A})(x)}~. $$
- Przykład: $\mathcal{D} = (\{a,b\},|.|)$, gdzie $|a|=1$ i $|b|=2$.
Mamy $\mathcal{D}(x) = x + x^2$, zatem $$Seq(\mathcal{D})(x) = \frac{1}{1-x-x^2}$$ Porównując z funkcją tworzącą liczb fibonacciego otrzymujemy $D_n = F_{n+1}$ - Przykład: $\mathcal{N}^{+} = (\{1,2,3,4,\ldots,|.|)$, gdzie $|n|=n$. Mamy $\mathcal{N}^+(x) = \frac{x}{1-x}$. Zatem $$ Seq(\mathcal{N}^+)(x) = \frac{1}{1-\frac{x}{1-x}} = \ldots = 1+\frac{x}{1- 2x} = \ldots = 1+\sum_{n\geq 1}2^n x^n $$ Zadanie: Podaj interpretację kombinatoryczną tego wyniku.
- Multizbiory. Mamy klasę $\mathcal{A}$ taką, że $a_0=0$. Niech $A = \{b_n:n\in\NN\}$. Dla wyrażeń formalnych postaci $$ x = \sum_n \alpha_n b_n $$ takich, że $\alpha_i \in \NN$ oraz $\sum_n \alpha_n \lt \infty$ określamy $$ |x| = \sum_n \alpha_n |b_n| $$ Tak określoną strukturę oznaczamy przez $Mult(\mathcal{A})$.
- Tw. $Mult(\mathcal{A})(x) = \prod_{a\in A} \frac{1}{1- x^{|a|}}$
- Przykład. Jeśli $\mathcal{A} = (\{a_1,\ldots,a_n\},|.|)$, gdzie $|x|=1$ to $$ Mult(\mathcal{A})(x) = \frac{1}{(1-x)^n} = \sum_k\binom{-n}{k}(-x)^k = \sum_k\binom{k+n-1}{k}(x)^k = \sum_k\multiset{n}{k}x^k~, $$ otrzymaliśmy więc znany już wzór z Wykładu 8.
- Przykład. Chcemy obliczyć na ile sposobów mogę 100 zł wyrazić za pomocą 1 zł, 2 zł i 5 zł.
Rozważamy klasę $\mathcal{A} = (\{1,2,5\},|.|)$, gdzie $|x|=x$. Mamy $$ Mult(\mathcal{A})(x) = \frac{1}{1-x}\frac{1}{1-x^2}\frac{1}{1-x^5} $$ Rozwijamy $Mult(\mathcal{A})(x)$ w szereg Taylora w punkcie 0 za pomocą dowolnego narzędzia, znajdujemy współczynniki przy $x^{100}$; okazuje się, że jest on róny 541.
03.06.2022: Klasy kombinatoryczne - III.
- Cykle: Jeśli $\mathcal{A}$ jest klasą kombinaroryczną bez elementów rozmiaru $0$ to
$$Cycle(\mathcal{A})(x) = \sum_{n \geq 1}\frac{\phi(n)}{n} \ln \frac{1}{1-\mathcal{A}(x^n)}$$gdzie $\phi(n) = |\{k\in\{1,\ldots n\}: nwd(k,n)=1\}|$ (funkcja "phi" Eulera).
- Przykład: Rozważamy klasę $\mathcal{A} = (\{a,b\},|\cdot|)$, gdzie $|a|=|b| = 1$. Mamy $\mathcal{A}(x) = 2 x$. Więc $$ Cycle(\mathcal{A})(x) = \sum_{n \geq 1}\frac{\phi(n)}{n} \ln \frac{1}{1-2x^n} = \sum_{n \geq 1}\sum_{k\geq 1}\frac{\phi(n)}{n}\frac{1}{k}2^k x^{nk} = $$ $$ = \sum_{m\geq 1} x^m \frac{1}{m} \sum_{n\cdot k=m}\phi(n)2^k~. $$ Zatem, dla dowolnej liczby pierwszej $p$ mamy $$ [x^p]Cycle(\mathcal{A})(x) = \frac{1}{p} \left(2^p + (p-1)\cdot 2\right)~. $$
- Przykład: $\sum_n\sum_{k}\binom{n}{k}x^k y^n = \frac{1}{1-(x+1)y}$
- Twierdzenie Lagrange'a o inwersji [LIT].
Załóżmy, że $\phi$ jest analityczna w otoczeniu zera i $\phi(0)\neq 0$. Istnieje wtedy funkcja $f$ analityczna w otoczeniu zera taka, że
$$
f(x) = x \cdot \phi(f(x))
$$
dla $x$ z tego otoczenia. Co więcej:
$$[z^n]f[x] = \frac{1}{n}[u^{n-1}] \left(\phi(u)\right)^n$$
- Drzewa binarne:
- Równanie rekurencyjne dla klasy: $\mathcal{B} = \{\circ\} + \mathcal{B} \times \{\circ\}\times \mathcal{B}$
- Równanie dla funkcji tworzącej: $B(x) = x + B(x)\cdot x \cdot B(x) = x\cdot(1 + B(x)^2) = x\cdot\phi(B(x))$, gdzie $\phi(x) = 1+x^2$
- Z LIT otrzymujemy $[x^{2m+1}]B(x) = \frac{1}{m+1}\binom{2m}{m} (=C_m)$
10.06.2022: Grafy.
- Pojęcie grafu prostego i grafu
- Pojęcie rzędu wierzchołka
- Tw (Euler) Jeśli $\mathcal{G} = (V,E,\phi)$ jest grafem to
$$\sum_{v\in V} \text{deg}(v) = 2\cdot |E|$$
- Pojęcie ścieżki i drogi w grafie
- Pojęcie składowych spójnych w grafie.
- Tw. Jeśli graf prosty jest spójny, to
$$|E| \geq |V|-1$$
- Pojęcie drzewa
- Metody wyznaczania liczb Fibonacciego: